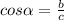⇒ b = c*cos 30° ⇒ 
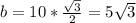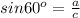
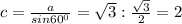см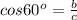
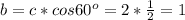см
см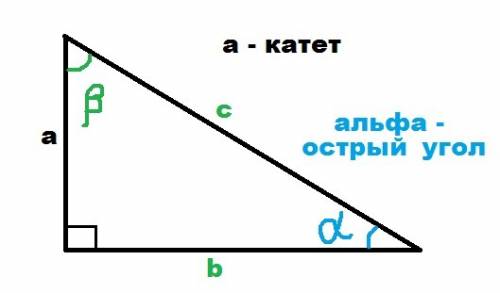
Примем сторону основания за а.
Проекция бокового ребра на основание равна (2/3)h = (2/3)*(a√3/2) =
a√3/3.
Высота H пирамиды как катет, лежащий против угла 60 градусов, равна:
H = (2/3)h*tg 60° = (a√3/3)*√3 = a.
Площадь основания So = a²√3/4.
Используем формулу объёма пирамиды:
V = (1/3)SoH = (1/3)(a²√3/4)*a = a³√3/12.
Зная, что V = 48, находим сторону основания.
a = ∛(12V/√3) = ∛ (12*48)/√3 = 4∛(9/√3) =4∛(√27) = 4√3.
Периметр основания Р = 3а = 12√3.
Осталось найти апофему А.
Находим боковое ребро: L = (2/3)h/cos 60° = (a√3/3)/(1/2) = 2a√3/3.
Подставим значение а: L = 2*4√3*√3/3 = 8.
Тогда апофема А = √(L² - (a/2)²) = √(64 - 12) = √52 = 2√13.
Приходим к ответу: Sбок = (1/2)РА = (1/2)* 12√3*2√13 = 12√39 кв.ед.
1)Больший угол находится при вершине равнобедренного треугольника,тогда:
3х+102=180
3х=78
х=26
2х+102=154
2)Большие углы находятся при боковых сторонах ,тогда:
3х+51=180
3х=129
х=43
2х=86
ответ:Вариант 3