∠САВ=165°
Объяснение:
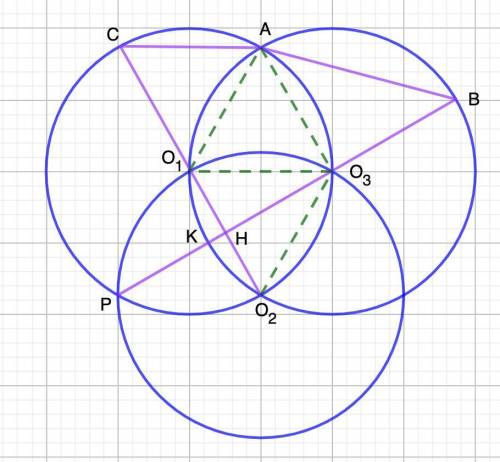
Соединим точки О₁ и А; А и О₃; О₁ и О₃; О₂ и О₃.
Так как три окружности проходят через центры друг друга ⇒их радиусы равны. Пусть радиусы всех окружностей равны R.
1. Рассмотрим Окр. О₁R и Окр. О₂R.
СО₂⊥РО₃ (свойство пересекающихся окружностей)
⇒∠СНВ=90°.
2. Рассмотрим ΔО₁АО₃
О₁А=АО₃=О₃О₁=R
⇒ΔО₁АО₃ - равносторонний.
⇒∠АО₁О₃=60°=∪ АО₃ (центральный)
3. Рассмотрим ΔО₂О₁О₃=равносторонний.
О₁О₃=О₃О₂=О₁О₂=R
⇒∠О₂О₁О₃=60°=∪ О₃О₂ (центральный)
4. ∪ АО₃О₂=∪ АО₃+∪ О₃О₂=60°+60°=120°
5. Рассмотрим Окр. О₁R.
∠О₂СА=120°:2=60° (вписанный)
6. Рассмотрим ΔО₁О₃О₂ равносторонний.
О₃Н⊥РО₃ (п.1)⇒О₃Н-высота, биссектриса (свойство равнобедренного Δ)
⇒∠НО₃О₁=30°=∪ О₁К (центральный)
7. ∠О₁О₃А=60° (ΔО₁АО₃-раввносторонний)
⇒∪ АО₁=∠О₁О₃А=60° (центральный)
8. ∪ КО₁А=∠О₁О₃А+∠КО₃О₁=60°+30°=90°
∠КВА=90°:2=45°(вписанный)
9. Сумма углов четырехугольника равна 360°.
⇒∠САВ=360°-(90°+60°+45°)=165°
2) ΔABE - равнобедренный ⇒ Опустим из точки В на основание АЕ высоту ВН ⇒ АН = НЕ = AE/2 = 8 см.
Высота равнобедренного треугольника, проведенная к его основанию, является медианой и биссектрисой.
CB⊥α ⇒ CB⊥(ABE)
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости.
CB⊥AB, CB⊥BE, CB⊥AE, CB⊥BH
ΔCBA = ΔCBE по двум катетам:
СВ - общая сторона
АВ = ВЕ - из равнобедренного ΔАВЕ
Значит, АС = СЕ ⇒ ΔАСЕ - равнобедренный.
В ΔАСЕ опустим из точки С на основание АЕ высоту. Высота должна пройти через середину АЕ, то есть через точку Н.
Следовательно, расстояние от точки C до стороны треугольника AE равно СН, ρ (С;АЕ) = СН - искомое расстояние.
В ΔАВН (∠ВНА = 90°): По теореме Пифагора
АВ² = ВН² + АН²
ВН² = АВ² - АН² = 10² - 8² = 100 - 64 = 36
ВН = 6 см
В ΔСВН (∠СВН = 90°): По теореме Пифагора
СН² = СВ² + ВН² = 4² + 6² = 16 + 36 = 52
Значит, СН = √52 = 2√13 см.
ответ: 2√13 см
3) а) AD ⊥ пл. АВС, следовательно, AD ⊥ СВ;
AD ⊥ BC, AC⊥ CB, то по теореме о 3-х перпендикулярах DC ⊥ ВС, то есть треугольник CBD - прямоугольный.
б) DCB = 90*, BD2 = DC2 + BC; BD = (вектор)4 + 6 = 10
Объяснение:
Sосн=пи*r²= пи*16
H=3*V/S=81/16
Осевое сечение конуса -треугольник с основанием- диаметром, и высотой к этому основанию- высота конуса: Sсеч=1/2 *8* 81/16= 81/4