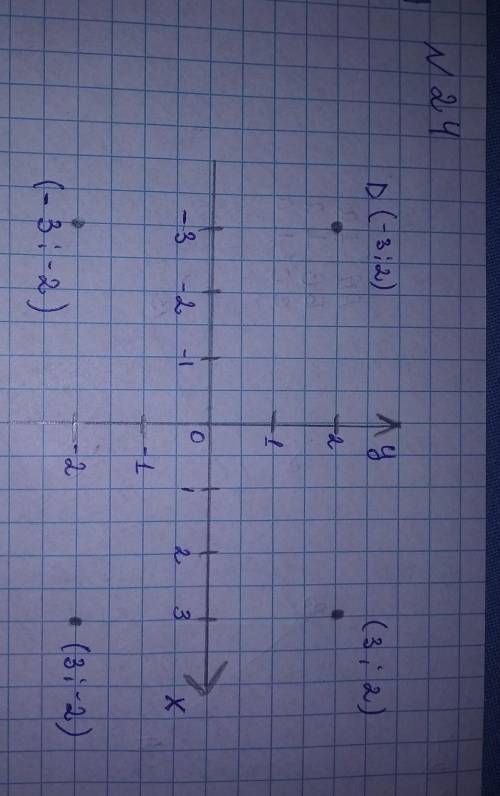
№24
а) точка симметричная относительно начала координат (3;-2)
б) точка симметричная относительно оси ОХ (-3;-2)
точка симметричная относительно оси ОУ (3;2)
(когда делаешь семетрию относительно
• начала координат нужно поменять знаки + на -, и - на + у: "х" и "у"
• оси ОХ знак нужно поменять только у: "у"
• оси ОУ знак нужно поменять только у: "х")
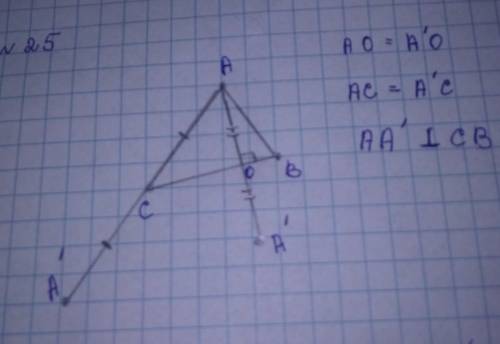
№25
а) симметрично относительно вершины С
нужно продлить сторону АС в направлении точки С в два раза и на конце мы получим точку А'
у нас получается прямая АА' и точка С которая делит эту прямую пополам
б) симметрично относительно стороны прямой ВС
проводим высоту из точки А до стороны ВС и обозначаем там точку О
дальше нужно продлить нашу высоту АО в 2 раза и в конце поставить точку А'
у нас будет прямая АА' которая перпендикулярная прямой ВС и точкой их пересечения делиться пополам
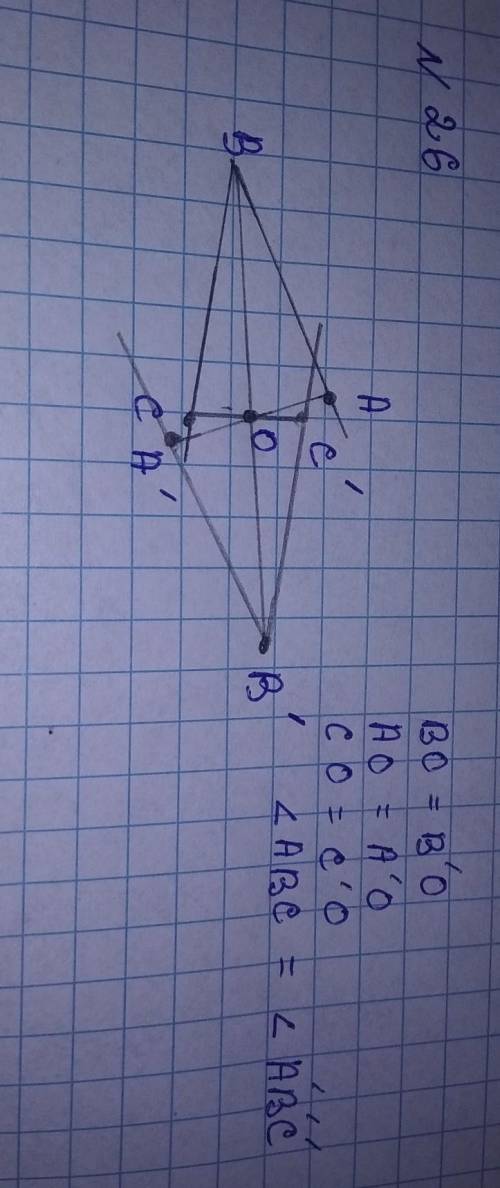
№26
из каждой точки угла проводим прямую до точки О
продолжу прямую в два раза так что точка О делит мои прямые пополам
и на них в соответствии ставлю точки А', В', С' и соединяю их по порядку
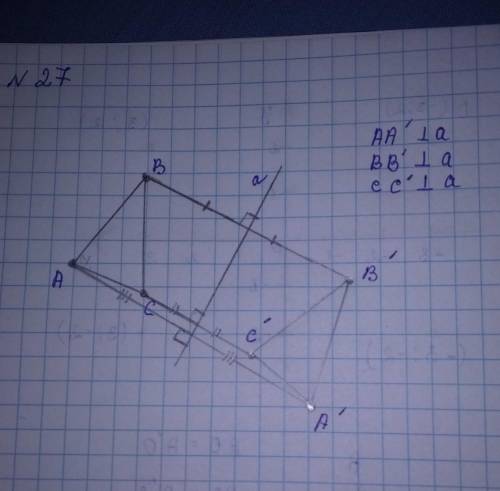
№27
из каждой вершины треугольника провожу перпендикуляр до прямой "а"
продолжу перпендикуляры в два раза и на их концах поставлю точки А', В', С' и соединяю их по порядку
(рисунки прикрепляю к каждому заданию)
надеюсь всё будет понятно
30 000тг
Опустим перпендикуляр на основание из верхней точки. Какова его длина?
В равнобедренном треугольнике перпендикуляр на основание яв-ся также биссектрисой и медианой, значит фронтон будет поделен на 2 прямоугольных треугольника с такими параметрами
гипотенуза - 5м
один из катетов - 8/2=4м
Сразу, не думая говорим, что это египетский треугольник и второй катет равен 3.
Но можете посчитать по т. Пифагора.
Теперь вычисляем площадь фронтона:
Площадь равна половине основания умноженной на высоту.
S=8*3/2=12м²
Теперь осталось уплатить строителям, которые уже давно все посчитали
12*2500=30 000тг
Так как высота прямоугольного треугольника равна среднему геометрическому
отрезков гипотенузы, на которые она ее разбивает, то можно записать
h=√AH*HB или h^2=AH*HB=6AH. (1)
C другой стороны, по теореме Пифагора из прямоугольного ACH h^2=AC^2-AH^2=
=16-AH^2. Подставим это в уравнение (1) и получим
6AH=16-AH^2. Решая это квадратное уравнение, получаем,что AH=2 (см)(второй корень не подходит, так как он отрицательный).
Теперь можно найти и высоту h данного треугольника: h=√16-4=2√3 (см).
Площадь треугольника ABC: S(ABC)=1/2*h*AB=1/2*2√3*8=8√3 (см^2).
ответ:8√3