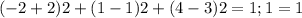, значит точка А(-2; 1; 4) Лежит на сфере, заданной уравнением (x+2)2+(y-1)2+(z-3)2=1.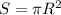 
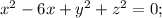
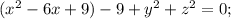
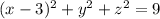- уравнение окружности
ОБРАТНОЕ УТВЕРЖДЕНИЕ:
Если высота, проведённая к стороне (именно "стороне", потому что мы ещё не доказали, что треугольник равнобедренный) треугольника делит эту сторону пополам, то такой треугольник равнобедренный.
Дано: ΔАВС, ВН- высота, АН=НС
Доказать: АВ=ВС
Доказательство: ΔАВН и ΔСВН - прямоугольные, так как ВН - высота.
ΔАВН=ΔСВН по первому признаку равенства треугольников (АВ=ВС, ВН- общая сторона, угол ВНА = углу ВНС=90⁰), значит АВ=ВС, и Δ АВС равнобедренный.
Ну и, как "Лучшее решение" не забудь отметить, ОК?!... ;)))
АВ∧2=АС∧2+ВС∧2 ⇒
АС∧2=АВ∧2-ВС∧2⇒АС=√АВ∧2-ВС∧2
АС=√13-9=√4=2
2) найдем tg <a, он равен отношению противолежащего катета к прилежащему, т.е.
СВ к АС
tg<a=CB\AC
tg<a=3\2=1,5