Пусть прямоугольник будет АВСД, а окружность имеет центр О.
Короткая сторона прямоугольника СД = АВ равна диаметру окружности (10см), следовательно, длинная сторона ВС=АД прямоугольника равна 17см.
Отрезок ОВ наклонён по углом 45°к сторонам АВ и ВС, поэтому ОВ √R² + R² = 5 √2.
ОА = ОВ = 5√2.
ОС = ОД = √((17 - 5)² + 5²) = √(144 + 25) = 13
Сумма расстояний от О до А, В, С, Д равна:
ОА +ОВ +ОС +ОД = 5√2 + 5√2 + 13 + 13 = 26 + 10√2
ответ: сумма расстояний от центра круга до вершин прямоугольника равна
(26 + 10√5)см
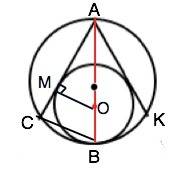
Обозначим хорды АС и АК. Они - касательные, проведенные к меньшей окружности.
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
⇒. ∠САВ=∠КАВ=60°:2=30°
Проведем СВ и КВ.
∠АСВ=∠АКВ=90° - опираются на диаметр АВ.
∆ АСВ=∆ АКВ - по гипотенузе и острому углу
⇒ АС=АК,
Проведем радиус ОМ в точку касания окружности с АС. Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒
∠АМО=90°
ОМ=r и противолежит углу 30°. ⇒ гипотенуза ОА=2r.
Тогда АВ=3r ⇒
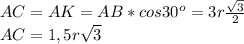
Одна из оснований всегда больше другой.
Сумма внутренних углов, как и у любого четырехугольника равна 360 градусам.
Равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. У равнобокой трапеции углы при основаниях равны. Диагонали равны. Два угла у большего основания острые, два угла у меньшего основания - тупые (это не оскорбление!).
Прямоугольной называется трапеция у которой одна боковая сторона перпендикулярна основаниям. Заметили, у прямоугольной трапеции 2 (два) прямых угла, а не один, как говорится в слабо продуманных определениях. Высота прямоугольной трапеции - это перпендикулярная к основаниям боковая сторона.