Условия не достаточно. Вокруг а1b1ab можно описать окружность у которой ab -диаметр. Отрезок а1b1-равен радиусу. Угол a1bb1 равен 30 градусам (половина центрального угла). Если угол abc=сab, то abc равен 60.
Значит угол abc - любой из диапазона (30, 90) градусов.
Угол стремится к 90, когда второй угол стремится к 30, т.е. треугольник становится прямоугольным, а b1a1 его высота к гипотенузе (точки b и b1 совпадают и b1a1 равен ba/2)
Вот если треугольник не просто острый, а равнобедренный, то abc=60 градусам.
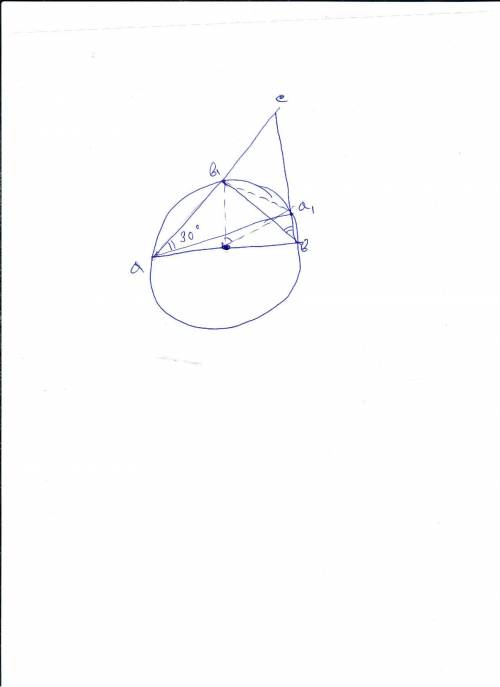
Условия не достаточно. Вокруг а1b1ab можно описать окружность у которой ab -диаметр. Отрезок а1b1-равен радиусу. Угол a1bb1 равен 30 градусам (половина центрального угла). Если угол abc=сab, то abc равен 60.
Значит угол abc - любой из диапазона (30, 90) градусов.
Угол стремится к 90, когда второй угол стремится к 30, т.е. треугольник становится прямоугольным, а b1a1 его высота к гипотенузе (точки b и b1 совпадают и b1a1 равен ba/2)
Вот если треугольник не просто острый, а равнобедренный, то abc=60 градусам.

В четырехугольнике АВСD ∠ВАD=∠BCD=90°
∠ADС=∠ADB+∠CDB=90°
Сумма углов четырехугольника 360°.=>
∠АВС=360°-3•90°=90°
Четырехугольник АВСD - прямоугольник. Противоположные стороны прямоугольника параллельны. => АВ║СD
или:
∆ АВD прямоугольный, угол АDB=15°,⇒ ∠ABD=90°-15°=75°
Углы, образованные прямыми АВ и СD и секущей BD, – накрестлежащие и равны.
По признаку параллельности прямых АВ║CD, ч.т.д.