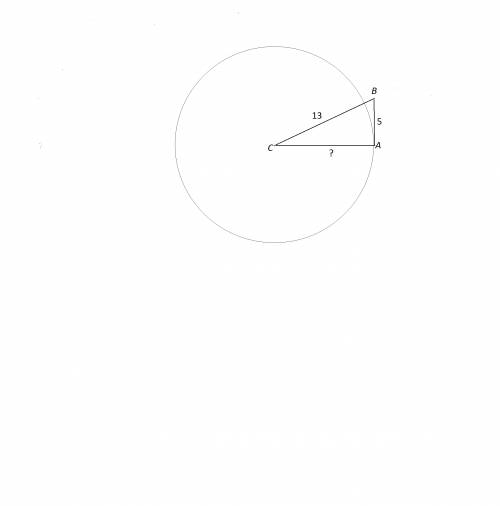
Если сделать рисунок, то будет понятно, что радиус этой окружности - катет АС данного прямоугольного треугольника.
Если окружность имеет с прямой только одну общую точку, то эта прямая - касательная к этой окружности.
Вершина угла А - точка касания.
Радиус окружности найдем по теореме Пифагора или вспомнив, что три стороны этого треугольника из так называемых троек Пифагора с отношением сторон 5:12:13.
------------------------------------------------------------------------------------------------------------------------------------
Треугольник, длины сторон которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, то есть, все его стороны и площадь являются целыми числами.
----------------------------------------------------------------------------------------------------------------------------------------
Катет АС=12 см, и является радиусом данной окружности
DE-медиана наклонённой грани
2)tgβ=H/AE⇔AE=H/tgβ
AE-медиана, опущенная из угла α
3)sin(α/2)=CE*tgβ/H⇔CE=H*sin(α/2)/tgβ
СE-половина катета, который лежит против угла α
4)AC²=(H²/tg²β)-(H²sin²(α/2)/tg²β)=H²(1-sin²(α/2))/tg²β
AC=H*cos(α/2)/tgβ
AC-катет, прилежащий к углу α
5)Sосн=H*cos(α/2)*2*H*sin(α/2) / 2*tg²β = H*cos(α/2)*sin(α/2) / tg²β
6)V=H*cos(α/2)*sin(α/2)*H / 3*tg²β = H²*cos(α/2)*sin(α/2) / 3*tg²β