Четырёхугольник ABCD вписан в окружность.
∠В : ∠D = 1 : 5
∠A < в 2 раза ∠С.
Найти:∠А - ? ; ∠В - ? ; ∠С - ? ; ∠D - ? .
Решение:Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
Около четырёхугольника ABCD описана окружность, по условию ⇒ ∠B + ∠D = 180˚; ∠A + ∠C = 180°.
Найдём ∠B и ∠D:
Пусть х - ∠В, тогда 5х - ∠D. (∠B : ∠D = 1 : 5, по условию)
Как я написала ранее, ∠B + ∠D = 180˚, по свойству.
х + 5х = 180
6х = 180
х = 30
30° - ∠B.
⇒ ∠D = 30˚ * 5 = 150˚.
Найдём ∠А и ∠С:
Пусть х - ∠А, тогда 2х - ∠С.
Как я написала ранее, ∠А + ∠С = 180°, по свойству.
х + 2х = 180
3х = 180
х = 60
60° - ∠А.
⇒ ∠С = 60° * 2 = 120°
ответ: 30°; 150°; 60°; 120°.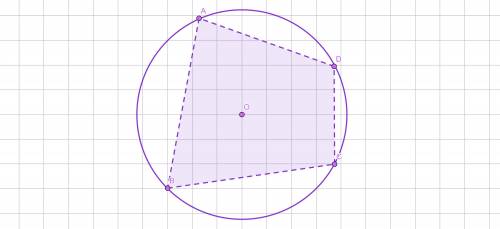
Объяснение:
Для начала проведем высоту из угла в 135° к большей высоте
Рассмотрим получившийся треугольник.
Т.к. у нас была дага трапеция, то острый угол её равен 45°
Тогда в получившемся треугольнике будут дава угла, равных 45°. Тогда этот треугольник является равнобедренным.
Значит, высота, проведённая к большему основанию, равна одной из отсекаемых частей (проекции).
Т.к. у нас первоначально трапеция была прямоугольной, то меньшая боковая сторона равна высоте и этой проекции.
Большее основание тогда равно сумме меньшего основания и проекции:
12 + 7 = 19.
ответ: 19.
и высчитываем по формуле
S=число пи* r^2
если r=5
S=3,14*25=78,5
ответ: 78,5