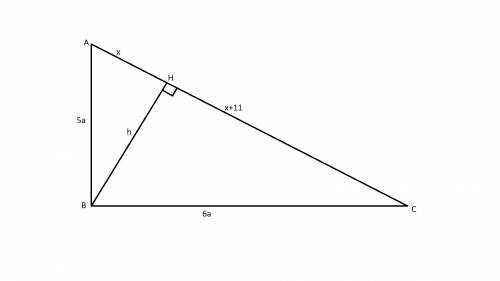
Дано:
прямоугольный треугольник АВС.
Высота из прямого угла ВН
НС=АН+11
ВС/АВ=6/5
1. Обозначим отрезок АН за х, тогда НС=х+11
По теореме Пифагора ВС²+АВ²=АС²
Выразим длины катетов через а:
ВС=6*а, АВ=5*а
(6а)² + (5а)² = (2х+11)²
61а²=(2х+11)²
2. Выразим высоту h через треугольник АВН: h²=25a²-x²
и подставим полученное значение в треугольник ВНС:
h²+(x+11)²=36a²
25a²-x² + (x²+22x+121)=36a²
сокращаем выражение и получаем: а²=2х+11
3. Подставляем выражение, полученное во втором действии в выражение, полученное в первом действии:
61(2х+11)=(2х+11)²
61=2х+11
Заметим, что 2х+11=с - гипотенуза треугольника АВС.
ответ: с=61 см.
So = a²√3 / 4 = 2²√3 / 4 = √3.
Такую площадь имеют все грани пирамиды, а их 4.
Поэтому полная поверхность пирамиды равна S = 4√3.
V = (1/3)*So*H.
Для определения высоты пирамиды надо рассмотреть прямоугольный треугольник, где гипотенуза - боковое ребро, а катеты - высота пирамиды и 2/3 части высоты основания (вершина правильной пирамиды проецируется в основании на точку пересечения медиан, они же и высоты и биссектрисы в треугольнике основания).
Н =√(2² - (2√3 / 3)²) = √(8/3) = 2√2 / √3.
Отсюда V = (1/3)*√3*(2√2 / √3) = 2√2 / 3.