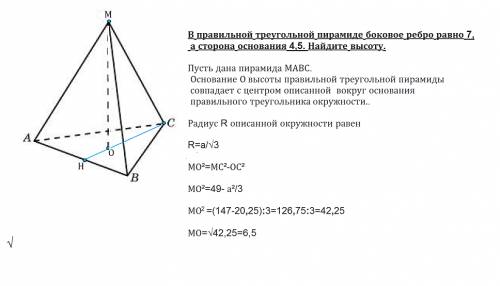
Обозначим пирамиду МАВС, МО - высота пирамиды. МО перпендикулярна основанию пирамиды.
О - центр описанной окружности около основания АВС данной пирамиды.
Все углы правильного треугольника равны 60°. По т.синусов радиус АО описанной окружности равен
R=AO:2sin60°
Если условие задано верно и сторона основания равна 4, то:
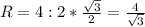
Тогда по т.Пифагора из прямоугольного ∆ АМО высота
МО=√(AM²-AO²)=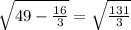
Но эта задача обычно задается со стороной основания, равной 4,5
Тогда условие задачи: В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания 4,5. Найдите высоту.
Для этого значения
R=4: 2√3/2=4,5:√3=1,5•√3
По т.Пифагора высота пирамиды
МО=√(МА²-АО²)=√(49-2,25•3)=6,5 (ед. длины)

Можно обойтись без рисунка, но с рисунком нагляднее.
Рассмотрим рисунок с трапецией АВСД.
Так как трапеция равнобедренная, а углы при основании равны 45°,
высоты из вершин В и С, опущенные на основание АД, отсекают от трапеции два равнобедренных прямоугольных треугольника АВН и СКД.
АН=ВН=СК=КД=АВ*sin(45)
АН=8*(√2):2=4√2
Высота равна 4√2,
АН=КД=4√2
ВС=НК=АД-2*АН=22-8√2
Полусумма оснований (ВС+АД):2=22+22-8√2=22-4√2
S (АВСД)=4√2(22-4√2)=88√2-32 см²