Дано: AB = 12см
BC = 13см
AC = 20см
A₁B₁ = 9см
Найти: B₁C₁
A₁C₁
По третьему признаку подобия треугольников: Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то они подобны.
Если \frac{AB}{A_1B_1}= \frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}
A
1
B
1
AB
=
B
1
C
1
BC
=
A
1
C
1
AC
, то Δ ABC ~ Δ A₁B₁C₁
Подставим значения сторон треугольника, которые уже знаем
\begin{gathered}\frac{12}{9}= \frac{13}{B_1C_1}=\frac{20}{A_1C_1}frac{4}{3}= \frac{13}{B_1C_1}=\frac{20}{A_1C_1}\end{gathered}
9
12
=
B
1
C
1
13
=
A
1
C
1
20
3
4
=
B
1
C
1
13
=
A
1
C
1
20
Теперь найдём стороны B₁C₁ и A₁C₁
B_1C_1=13:\frac{4}{3}=13*\frac{3}{4}=\frac{39}{4}=9\frac{3}{4}=9,75B
1
C
1
=13:
3
4
=13∗
4
3
=
4
39
=9
4
3
=9,75
A_1C_1=20:\frac{4}{3}=20*\frac{3}{4}=\frac{60}{4}=15A
1
C
1
=20:
3
4
=20∗
4
3
=
4
60
=15
ответ: A₁B₁ = 9см
B₁C₁ = 9,75см
A₁C₁ = 15см
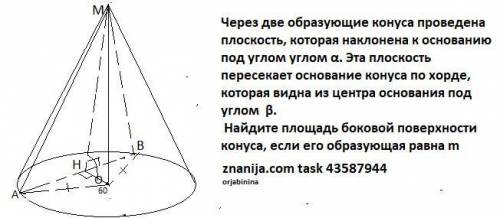
Через две образующие конуса проведена плоскость, которая наклонена к основанию под углом углом α. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под углом β. Найдите площадь боковой поверхности конуса, если его образующая равна m
Объяснение:
1) Пусть МА=МВ=m -образующие конуса, МО-высота конуса, МО⊥(АОВ) АВ-хорда , ∠АОВ=β. Проведем ОН⊥АВ , тогда МН⊥АВ , по т. о трех перпендикулярах ⇒ ∠МНО-линейный угол между основанием и плоскостью (АВМ), ∠МНО=α .
2) S(бок.конуса )= π * r* l . где r-радиус основания, l-образующая конуса. По условию l =m . Найдем r.
3)В равнобедренном ΔАОВ, высота является биссектрисой ⇒∠АОН=β/2. Получили ΔАОН- прямоугольный :
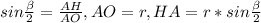 ,
,
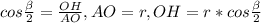 .
.
4) ΔMHO- прямоугольный : 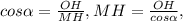 или
или 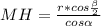 .
.
5) ΔAMH- прямоугольный ,по т. Пифагора НА²+МН²=МА² ,
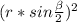 +
+ 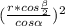 = m² ,r²(
= m² ,r²( 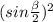 +
+ 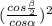 )=m² ,
)=m² ,
r = 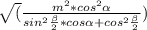 =
= 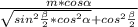 .
.
6) S(бок.конуса )= π * 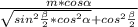 *m
*m
S(бок.конуса )= 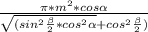 ( ед²) .
( ед²) .
10√4= 10⁴×2
10 в квадрате равно 10²