1)
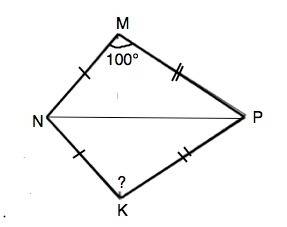
Проведем диагональ NP. Треугольники PMN и PKN равны по трем сторонам - две по условию, третья - общая. .
Следовательно, углы при вершинах К и М равны. Угол К=100°
2)
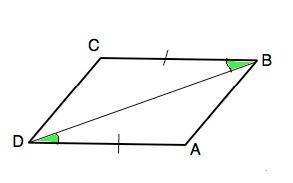
Диагональ BD делит четырехугольник на треугольники ∆ ABD и ∆ CBD. В этих треугольниках стороны ВС=АD по условию, DB общая, углы между этими сторонами равны. ∆ ABD и ∆ CBD равны по первому признаку равенства треугольников.
Следовательно, стороны АВ=CD.
Если противоположные стороны четырехугольника равны, этот четырехугольник - параллелограмм. ⇒, АВ||CD. Доказано.
ответ: 6√3 см
Объяснение:
Стороны ромба равны. Диагонали являются его биссектрисами и пересекаются под прямым углом.
Обозначим ромб АВСD. ВD=6. ВД=АВ ⇒ ∆ АВD=∆ BCD – равносторонние. Острые углы такого ромба равны 60°, тупые 2•60°=120°. Диагональ АС=АО+ОС
АО=ОС - высоты равных равносторонних треугольников.
АО=АВ•sin60°=6•√3/2=3√3
AC=2•3√3=6√3 см.
Тот же результат получим по т.Пифагора.