ответ: 560 см².
Объяснение:
Площадь полной поверхности прямой призмы-равна сумме площадей основания и боковой поверхности призмы.
S основания =1/2ab, где а и b - катеты.
S основания =1/2*8*15=60 см².
Боковая поверхность равна произведению периметру основания на высоту призмы.
Р основания =a+b+c. Найдем с - гипотенузу прямоугольного треугольника.
По т. Пифагора с=√8²+15²=√64+225 =√289=17 см. Тогда
S боковая = (8+15+17)*11=440 см².
И полная поверхность призмы равна
S полная = 2S основания + S боковая = 2*60+440= 560 см².
Объяснение:
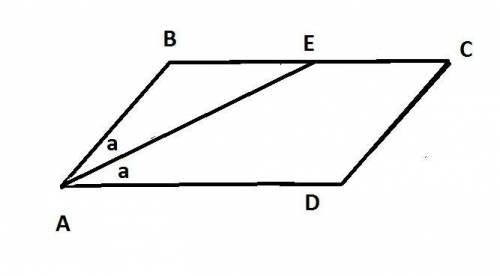
1) рассмотрим случай когда BE=5cм ; CE=6см
BC=5+6=11cм
Обозначим ∠BAE=a тогда ∠ЕAD=a так как АЕ - биссектриса и А=2a
сумма углов параллелограмма прилежащих к одной стороне=180°
A+B=180°; B=180°-A=180°-2a
рассмотрим ΔАВЕ
сумма углов треугольника =180°
∠BAE+∠B+∠BEA=180°
∠BEA=180°-∠BAE-∠B=180°-a-(180°-2a)=180°-a-180°+2a=a
∠BEA=a и ∠BAE=a
если в треугольнике два угла равны то он является равнобедренным, а сторона к которой прилежат два равных угла является основанием
⇒ ΔАВЕ-равнобедренный AB=BE=5 см
BC=11cм ; AB=5см
в параллелограмме противоположные стороны равны
тогда периметр Р=2(АВ+BC)=2(5+11)=2*16=32 cм
Р=32 см
2) рассмотрим случай когда BE=6cм ; CE=5см
тогда АВ=BE=6cм
Р=2(АВ+BC)=2(6+11)=2*17=34 cм
Р=34 см