MN=6
Объяснение:
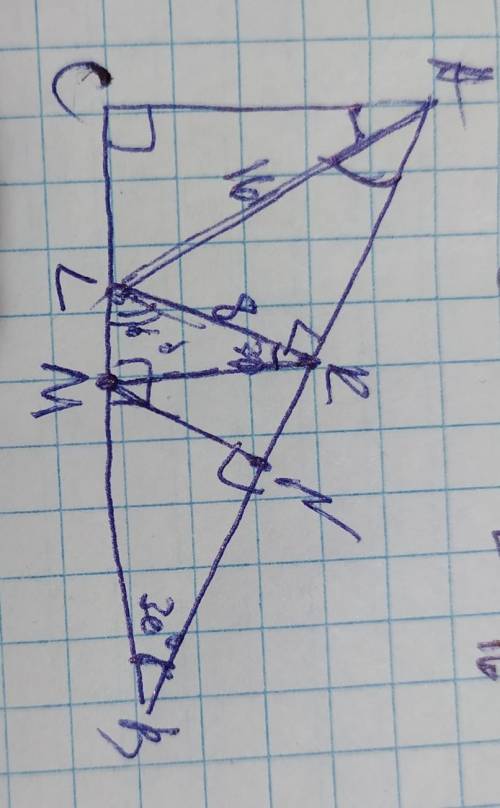
Сумма острых углов прямоугольного треугольника составляет 90°, и сли <В=30°, то <А=90–30=60°. Так как AL биссектриса, то <CAL=<KAL=60÷2=30°. Kаждая. высота, проведённая в каждом треугольнике, образуют другие треугольники, которые являются прямоугольными. В прямоугольном треугольнике катет, лежащий напротив угла В=30°, равен половине гипотенузы, поэтому в ∆ALK LK=½×AL=16÷2=8. Катет KL также является катетом в ∆LKB и гипотенуза ВL в ∆ LKB будет больше в 2 раза больше чем KL, поэтому ВL=8×2=16. Рассмотрим ∆LKB. Если угол В=30°, то угол BLK=60°(90–30=60), а <LKM в ∆LKM=30°, и катет LM=½×KL=½×8=4. Если BL=16, то ВМ=BL–ML=16–4=12. В ∆BMN ВМ - гипотенуза, а MN меньший катет, лежащий напротив угла В=30°, и поэтому равен ½× ВМ, поэтому MN=12÷2=6
3.
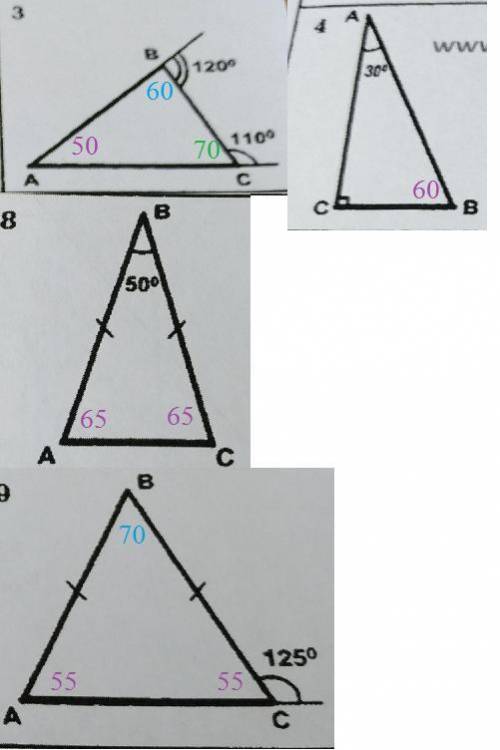
Cумма смежных углов 180 градусов.
Если один угол 120°, то второй 180°-120°=60°
Если один угол 110°, то второй 180°-110°=70°
Сумма углов треугольника АВС равна 180 градусов, два угла 60° и 70°, значит угол А равен 180°-60°-70°=50°
4.
Сумма острых углов прямоугольного треугольника равна 90°
Если один угол 30°, то второй 90°-30°=60°
8. Треугольник равнобедренный (АВ=ВС), значит углы при основании равны
Сумма углов треугольника равна 180°
180°-50°=130° - приходится на два угла при основании
130°:2=65°
9.
Cумма смежных углов 180 градусов.
Если один угол 125°, то второй 180°-125°=55°
Треугольник равнобедренный (АВ=ВС), значит углы при основании равны.
∠А=∠С=55°
Сумма углов треугольника равна 180°
180°-55°-55°=70° - третий угол треугольника
так как угол ВЕА=52°, то угол ЕВС тоже равен 52°
по условию угол АВЕ=СВЕ, то АВЕ тоже 52°
сумма углов треугольника =180°, следовательно угол ВАЕ=180-(52+52)=76°
ответ: угол А=76° В=52°, С=52°