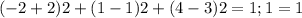, значит точка А(-2; 1; 4) Лежит на сфере, заданной уравнением (x+2)2+(y-1)2+(z-3)2=1. 
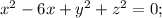
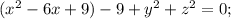
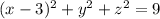- уравнение окружности
№1. Сторона правильной четырехугольной пирамиды равна а, а диагональное сечение - равносторонний треугольник. Найти объем пирамиды.
Пирамида QABCD, QO - высота, АQC- диагональное сечение, АВ=а.
V=S•h:3
S=a²
h=AC√3/2
AC=a:sin45°=a√2
h=a√6/2
V=a³√6/6
№2. Высота правильной четырехугольной пирамиды равна 12 см, а апофема – 15 см. Вычислить площадь боковой поверхности пирамиды.
Апофема – высота боковой грани правильной пирамиды, следовательно, QH⊥CD. По т. о 3-х перпендикулярах ОН⊥CD.
По т.Пифагора ОН=9 ( можно обойтись без вычислений, т.к. ∆ QOH- египетский, где отношение катет:гипотенуза=4:5).
ОН - половина АD, ⇒АD=2OH=18 (см)
Площадь боковой поверхности правильной пирамиды равна произведению апофемы на полупериметр основания.
S=15•18•4:2=540 см².
————————
№3. Условие неполное.
Объем V правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC), на высоту h (OS)
Формула площади основания S=a²√3/2. Зная высоту, несложно вычислить объём данной пирамиды.
———————
№4.
Сторона основания правильной треугольной пирамиды равна 8 см, а боковая грань наклонена к плоскости основания под углом 30°. Найти площадь полной поверхности пирамиды.
S(бок)=3•MH•AB:2=3•8/3•8:2=32
————————
№5
Основание пирамиды – треугольник со сторонами 13 см, 14 см, 15 см. Найти площадь сечения, которое проходит параллельно плоскости основания и делит высоту пирамиды в отношении 1:2, считая от вершины пирамиды.
————————
№6.
Найти объём правильной четырехугольной пирамиды, сторона основания которой равна 6 см, а диагональное сечение является равносторонним треугольником.
———————
Решения задач 4,5,6 даны в приложениях.
Объяснение:
В сечении получаем пятиугольник, который для определения площади можно разделить на равнобедренные треугольник и трапецию. Основание РМ этой фигуры равно 6√2.
Заданная плоскость пересекает рёбра ВВ1 и ДД1 в точках К и Т, расстояние между которыми равно диагонали квадрата основания, то есть 8√2.
Отрезок А1F является суммой высот указанных фигур.
Отрезок СF равен как высота из прямого угла 6*6/(6√2) = 6/√2 = 3√2.
Отсюда находим А1F = √(4² + (8√2 - 3√2)²) = √(16 + 50) = √64 = 8.
Расстояние (из подобия) ДТ = (2*4/(8 + 2) = 8/10 = 4/5.
Высота трапеции равна ДТ/cos(A1FA) = (4/5)/(4/8) = 8/5.
Тогда высота треугольника равна 8 - (8/5) = 32/5.
Получаем ответ: S = (1/2)*(32/5)*8√2 + ((8√2 + 6√2)/2)*(8/5) =
= ((32/5)*4√2 + 56√2)/5 = (184√2)/5 кв.ед.