Не могу нарисовать рисунок, но попытаюсь объяснить.
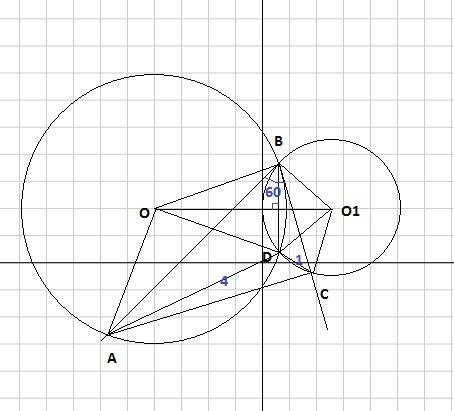
Пусть имеется прямоугольный треугольник ABC с гипотенузой AC и прямым углом при вершине В.
Пусть точка О – пересечение заданных биссектрис. Один из углов при О = 100 градусов
Вариант 1.
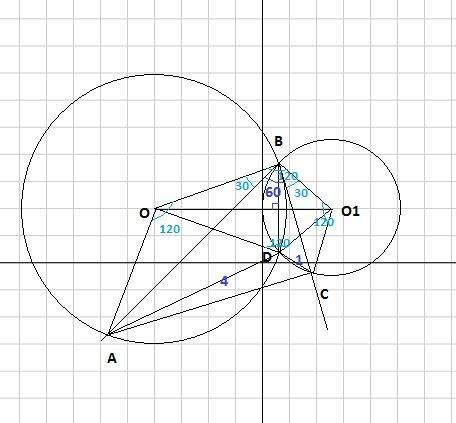
Расcмотрим треугольник ABO. Угол AOB=100, угол ABO=45 (потому что BO – биссектриса угла В, который 90 град)
Тогда угол BAO=180-100-45=35
Угол BAC вдвое больше BAO и равен 35*2=70.
Оставшийся уголACB =180-90-70=20.
Вариант 2.
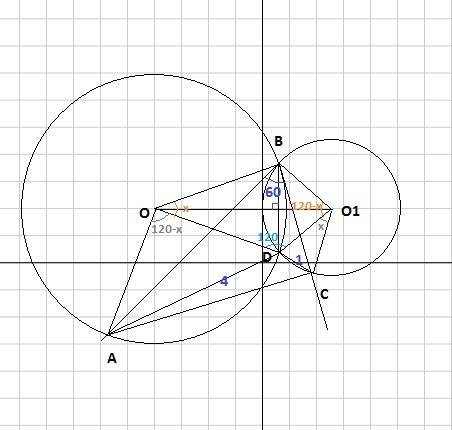
(если вдруг возникнет иллюзия считать, что распределение углов при точке О другое – то есть 100 град = угол AOD, где точка В – точка пересечения биссектрисы из вершины B со стороной AC, То в таком случае:
Всё равно рассмотрим треугольник ABO. Только угол AOB=180-100=80. угол ABO всё равно 45 (потому что BO – биссектриса угла В, который 90 град)
Тогда угол BAO=180-80-45=55.
Угол BAC в этом случае вдвое больше BAO и равен 55*2=110. И тут упс – сумма двух углов начального прямоугольного треугольника уже становится больше 180, а ведь есть ещё и третий угол. Поэтому распределение углов при точке О только такое, как в первом варианте решения. Второй вариант нежизне
AB=B-A=(-8+3;-5-4)=(-5;-9);
AC=C-A=(0+3;-7-4)(3;-11);
Сложение и вычитание векторов → сложение и вычитание их соответствующих координат, например AB-AC=AD(Xab-Xac;Yab-Yac)=(Xad;Yad);
AD=AB-AC=(-5-3;-9+11)=(-8;2);
Если координаты вектора → из координат точки конца вычесть соответствующие координаты точки начала (AD=D-A→D=AD+A), из имеющихся и полученных данных можно составить:
D=(-8;2)+(-3;4)=(-8-3;2+4)=(-11;6);
Точка D имеет координаты (-11;6).
Если я нигде не ошибся, то правильно)) )
(Это страничка сестры)!