78. ΔADB = ΔCDB по двум сторонам (AD = CD, а также общая сторона BD) и углу между ними (∠ADB = ∠CDB), то есть по первому признаку равенства треугольников.
79. ΔADB = ΔCDB по двум сторонам (AD = BC, а также общая сторона BD) и углу между ними (∠ADB = ∠CBD), то есть по первому признаку равенства треугольников.
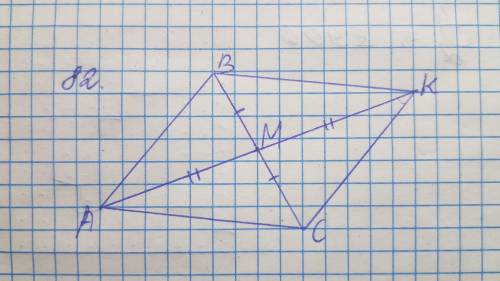
82. ΔACM = ΔKBM по двум сторонам (BM = MC, AM = MK) и углу между ними (∠BMK = ∠AMC, так как эти углы вертикальные), то есть по первому признаку равенства треугольников. Рисунок к задаче на фото.
86. ΔADB = ΔCDB по стороне (общая сторона BD) и двум прилежащим углам (∠ABD = ∠CBD, ∠ADB = ∠CDB), то есть по второму признаку равенства треугольников.
87. ΔADB = ΔCDB по стороне (общая сторона BD) и двум прилежащим углам (∠ABD = ∠CDB, ∠ADB = ∠CBD), то есть по второму признаку равенства треугольников.
сosA=AC/AB=15|25=3|5
Косинус внешнего угла по формулам приведения
cos(180-A)=-cosA=-3|5