Пусть О - середина отрезка АВ. Опустим перпендикуляры к плоскости из точек А, В и О, соответствующие точки на плоскости обозначим A', B' и O', отрезки АА', ВВ' и ОО' - параллельны.Так как проекция сохраняет отношение длин коллинеарных отрезков, то A'O'/O'B'=АО/ОВ=1, т.е.O' - середина A'B'. Получается, что А'АВВ' - трапеция, где А'А и В'В - основания, а О'О - её средняя линия. Длина средней линии трапеции равна полусумме длин её оснований.
(2,4+7,6):2=5 (см)
ответ: расстояние от середины отрезка АВ до плоскости 5 сантиметров.
Расстояние между основаниями столбов является проекцией перекладины на плоскость.
Столбы, перекладина и проекция перекладины на плоскость образуют прямоугольную трапецию. Если провести плоскость параллельную данной на высоте 3 метра, то получим прямоугольник и прямоугольный треугольник.
В этом прямоугольном треугольнике гипотенуза равна 5 м, а один из катетов равен 6-3=3(м).По теореме Пифагора найдём второй катет, который равен искомому расстоянию между столбами:
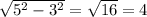 (м)
(м)
ответ: расстояние между основаниями столбов 4 метра.
Высота=образующей=5 см
Площадь основания=π*радиус²=4π (см²)
Объем=5*4π=20π (см³)