Дано: ABСD - прямоугольник.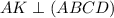 
. КВ=7 м, КD=8 м, КС=10 м.
Найти: АК.
Решение.
Пусть AD=а и AB=b - стороны прямоугольника.
Тогда по теореме Пифагора длина диагонали прямоугольника равна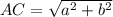 
м.
Пусть АК=x м - длина искомого перпендикуляра. Тогда по теореме Пифагора
Получаем уравнение с длиной прямоугольника
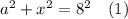
Уравнение с шириной прямоугольника
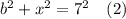
Уравнение с диагональю прямоугольника
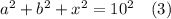
Сложим первое и второе уравнения. Получим
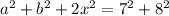
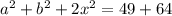
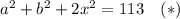
Вычтем из (*) уравнение (3). Получим
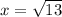
ответ: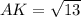 
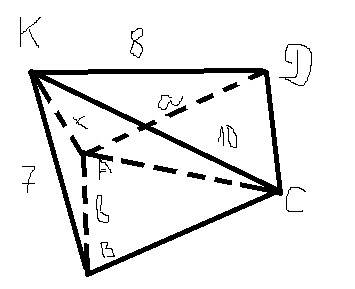
Треугольник KCD очевидно правильный, поэтому r = √7; - это треть высоты KCD, которая, очевидно является высотой и трапеции ABKD.
В эту трапецию можно вписать окружность, поэтому, если верхнее основание BK = x, а нижнее AD = a, то боковые стороны AB = KD = (a + x)/2; (суммы противоположных сторон равны).
Если продлить AB и KD до пересечения в точке Е, то AED - правильный треугольник, и окружность, вписанная в трапецию ABKD, является вписанной и в AED. Диаметр этой окружности равен 2/3 высоты AED, а высота EBK, соответственно, равна 1/3 высоты AED. Из очевидного подобия элементов трегуольников EBK и AED x = a/3;
то есть AB = KD = KC = 2*AD/3 = 2*a/3;
Из такого же подобия элементов треугольников AED и KCD следует, что радиус вписанной в трапецию окружности r1 = 3r/2; (то есть r/r1 = KC/AD)
Если центры окружностей O1(вписаная в AED радиуса r1 = 3r/2) и O2 (вписанная в KDC радиуса r), то точка O2 проектируется на AD в точку D, а точка O1 - в середину AD, поэтому, если O1O2 = p, то p^2 = (a/2)^2 + (r1 - r)^2;
При этом a/2 = (√3)*r1 = (3√3/2)*r;
Откуда p^2 = ((3√3/2)^2 + (1/2)^2)*r^2 = 7*r^2 = 7^2;
O1O2 = 7;
BD⊥AO как диагонали квадрата, ⇒
BD⊥(AA₁O).
Плоскость (BA₁D) проходит через BD, значит плоскости (AA₁O) и (BA₁D) перпендикулярны.
Проведем АН⊥А₁О.
АН∈ (AA₁O), ⇒ АН⊥BD, значит АН⊥(BA₁D).
АН - искомое расстояние.
АА₁ = 1,
АО = АС/2 = √2/2,
А₁О = √(АА₁² + АО²) = √(1 + 1/2) = √6/2 - по теореме Пифагора
АН = АА₁ · АО / А₁О (высота, проведенная к гипотенузе, равна отношению произведения катетов к гипотенузе)
АН = √2/2 / √6/2 = 1/√3 = √3/3