1152 см²
Объяснение:
1) Площадь ромба равна половине произведения его диагоналей:
S = 12 · 16 : 2 = 96 см².
2) Таких оснований - 2, соответственно:
S осн = 96 · 2 = 192 см².
3) Диагонали ромба пересекаются под углом 90° и в точке пересечения делятся пополам: половинки диагоналей вместе со стороной ромба образуют прямоугольный треугольник, в котором половинки диагоналей являются катетами, а сторона ромба - гипотенузой.
Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов:
с² =а² + b²
с² = (12/2)² + (16/2)² = 6²+8²=36+64=100,
с = √100 = 10 см - это сторона ромба.
4) В боковой грани диагональ 26 см является гипотенузой прямоугольного треугольника, а катетами являются сторона ромба (10 см) и высота параллелепипеда H, которую надо найти, чтобы вычислить площадь боковой поверхности.
Согласно теореме Пифагора, квадрат катета равен разности квадрата гипотенузы и квадрата другого катета:
H² = 26² - 10² = 676 -100 = 576,
Н = √576 = 24 cм.
5) Площадь боковой поверхности ромба равна произведению периметра его основания на высоту. Т.к. все стороны ромба равны 10 см, то его периметр равен 10 · 4 = 40 см.
Отсюда площадь боковой поверхности:
S бок = 40 · 24 = 960 см².
6) Площадь полной поверхности параллелепипеда равна сумме площадей его оснований и боковой поверхности:
S полн = S осн + S бок = 192 + 960 = 1152 см².
ответ: 1152 см².
ответ:ВН
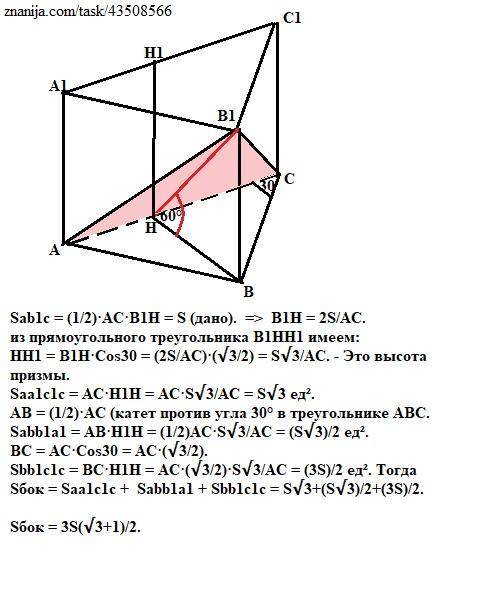
Sбок = 3S(√3+1)/2.
Объяснение:
Sab1с = (1/2)·AC·B1H = S (дано). => В1Н = 2S/AC.
Угол между двумя пересекающимися плоскостями (двугранный угол) равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.
Проведя высоты В1Н и ВН в треугольниках АВС и А1В1С1 соответственно (основания этих перпендикуляров совпадут по теореме о трех перпендикулярах) , получим прямоугольный треугольник В1НВ с углом ∠ВНВ1 = 60° (дано).
Из прямоугольного треугольника В1НН1 с углом Н1НВ1 = 30° (так как ∠Н1НВ=90°) имеем:
HH1 = B1H·Cos30 = (2S/AC)·(√3/2) = S√3/AC. - Это высота призмы.
Saa1c1c = AC·H1H = AC·S√3/AC = S√3 ед².
AB = (1/2)·AC (катет против угла 30° в треугольнике АВС.
Sabb1a1 = AB·H1H = (1/2)AC·S√3/AC = (S√3)/2 ед².
ВС = АС·Cos30 = АС·(√3/2) (из треугольника АВС).
Sbb1с1с = ВС·H1H = АС·(√3/2)·S√3/AC = (3S)/2 ед². Тогда
Sбок = Saa1c1c + Sabb1a1 + Sbb1с1с = S√3+(S√3)/2+(3S)/2.
Sбок = 3S(√3+1)/2.
Решение: Пусть АBCD – данный ромб, угол А=угол С=L.
Площадь ромба равна произведению квадрата стороны на синус угла между сторонами
S=AB^2 *sin A
S=a^2* sin L
Полупериметр робма равен полусумме сторон ромба
p=4*a\2=2*a
Площадь ромба равна произведению полупериметра на радиус вписанной окружности
S=p*r
Откуда
r=S\p= a^2* sin L \ (2*a)=a\2* sin L
Пусть X, Y – точки касания вписанной в ромб окружности со сторонами AB и AD соответсвенно , пусть H – точка пересечения, прямой FG, перпендикулярной к диагонали АС, вторая окружность касается сторон AB и AD и соприкасается с первой окружностью в точке H, значит вторая окружность – окружность вписанная в треугольник AFG.
Угол B=угол D=180 – угол А=180-L
Диагональ АС ромба равна по теореме косинусов
AC^2=AB^2+BC^2-2*AB*BC*cos B=
=a^2+a^2-2*a*a*cos (180-L)=2*a^2* (1+cos L)
AC=корень(2*a^2* (1+cos L))=2*а*|cos L\2|=2*a*cos (L\2)
(воспользовались формулой понижения квадрата косинуса)
Пусть О – центр вписанной в ромб окружности
Диагонали ромба пересекаються и в точке пересечения делятся пополам, причем точка пересечения является центром вписанной в ромб окружности(свойство ромба)
Значит АО=1\2*АС=1\2*2*a*cos (L\2)= a*cos (L\2)
Далее AH=AO-OH= a*cos (L\2) -a\2* sin L=a*cos (L\2)*(1-sin(L\2))
AF=AH\cos (A\2)= a*cos (L\2)*(1-sin(L\2)) \cos (L\2)=
= a*(1-sin(L\2))
FH=AH*tg (A\2)= a*cos (L\2)*(1-sin(L\2))*tg (L\2)= a*sin (L\2)*(1-sin(L\2))
FG=2*FH=2* a*sin (L\2)*(1-sin(L\2))
Треугольники AFH и AGH равны как прямоугольные за катетом и острым углом(угол FAH=угол GAH – диагональ ромба есть его биссектриссой – свойство ромба, AH=AH,
Прямая FG касательная к первой окружности, значит перпендикулярная к АС, отсюда углы FHA и GHA прямые).
Из равенства треугольников получаем AF=AG
Площадь треугольника равна произведению половины основания на висоту
Площадь треугольника AFH :
S (AFG)=FH*AH= a*sin (L\2)*(1-sin(L\2))* a*cos (L\2)*(1-sin(L\2))=
1\2*a^2 *sin L *(1-sin(L\2))*^2
Полупериметр треугольника равен
p (AFG)= (AF+FG+AG)\2=( a*(1-sin(L\2))+ a*(1-sin(L\2))+ 2* a*sin (L\2)*(1-sin(L\2)))\2=
a*(1-sin(L\2))+ a*sin (L\2)*(1-sin(L\2))= a*(1-sin(L\2))*(1+sin(L\2))=
a*(1-sin^2 (L\2))=a*cos^2 (L\2)
Радиус вписанной окружности в треугольник равен площадь\полуперимтер,
Радиус равен 1\2*a^2 *sin L *(1-sin(L\2))*^2 \( a*cos^2 (L\2))=
=a*tg (L\2)*(1-sin(L\2))^2
ответ: a*tg (L\2)*(1-sin(L\2))^2