1) Два противолежащих угла параллелограмма равны
Сумма внутрениих углов параллелограмма равны 360 градусов, отсюда мы найдем 360-(35+35)=290 - это сумма оставшихся двух углов равных между собой.
290/2=145
ответ: 145 градусов,35градусов,145градусов,35градусов.
2)Решаем схоже с первой 360-(100+100)=160сумма оставашихся двух углов
160/2=80градусов
ответ:100 градусов,80градусов,100градусов,80градусов
3) Решаем с уравнения
х- угол
2х*2+х+х=360
4х+2х=360
6х=360
х=360/6
х=60
Сказано что в 2 раза больше, значит:60*2=120(больший угол в параллелограмме)
ответ:120градусов,60градусов,120градусов,60градусов
4)Составляем уравнение
(х+90)*2+х+х=360
2х+180+2х=360
4х+180=360
4х=360-180
4х=180
х=180/4
х=45
45+90=135(большая сторона)
ответ:135градусов,45градусов,135градусов,45градусов
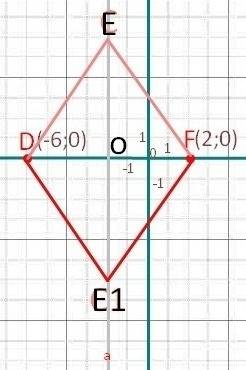
Чертим систему координат, на ней отмечаем данные точки.
Из просчётов видно, что отрезок, являющийся стороной равностороннего треугольника AEF = |-6| + |2| = 8. Модули здесь - отклонения от нулевой точки системы координат по оси абсцисс. Ординат тут равен нулю, так что не входит в счёт.
Для чертежа ищем середину отрезка DF: 8:2 = 4. На оси X это точка -2.
Чертим параллельную оси Y прямую, проходящую через точку -2 на оси X. (на рисунке она серая)
К ней с чертёжных принадлежностей дорисовываем два отрезка длиною 8, такие, чтобы их концы были в точках D и F, соединялись в точке Е или Е1.
А теперь сами просчёты:
Рассмотрим треугольник OЕF:
ЕF = 8, ОF = 4. найдём OE по теореме Пифагора: OE²=8²+4²=80.
OE = √80 = 4√5 ≈ 9.
Т.к. треугольник может отклоняться как вверх, так и вниз, точек E и E1, которых не хватало для образования треугольника DEF, оказалось две.
Таким образом, искомые точки: E(-2;9) и E1(-2;-9).
а) мы выяснили, что один угол равен 81, другой по условию задачи - 40, значит, третий угол 180-81-40=59, (81,40,59)
б) один угол равен 81, значит, сумма двух других 180-81=99. Соотношение этих углов 2:7, то есть мы можем обозначить один угол как 2х, другой как 7х. А если их сумма известна, томы можем составить уравнение 2х+7х=99, 9х=99, х=11. Таким образом один из этих углов 2*11=22, другой 7*11=77, (81,77,22)
в) один из неизвестных углов обозначим х, тогда другой будет равен (х+51). Мы знаем сумму углов, поэтому можем составить уравнение х+х+51=99, 2х=48, х=24 - один угол, 24+51=75 - другой угол, (8,24,75)
г) известный нам угол в 81 градус может быть углом при вершине, тогда два других угла - углы при основании и они равны, т.к. треугольник равно бедренный, значит 99:2=49,5 (81;49,5;49,5)
угол в 81 градус может быть углом при основании, тогда другой угол при основании также равен 81, значит угол при вершине 180-81-81=18 (81,81,18)