Северный Ледовитый океан — самый маленький из океанов, его площадь 14,75 миллионов км², то есть чуть больше 4 % от всей площади Мирового океана. Объём воды составляет 18,07 миллионов км³. Некоторые океанографы рассматривают его как одно из морей Атлантического океана. Северный Ледовитый океан самый мелководный из всех океанов, его средняя глубина составляет 1225 м (наибольшая глубина 5527 м в Гренландском море)[1][6].
Расположен между Евразией и Северной Америкой. Граница с Атлантическим океаном проходит по восточному входу Гудзонова пролива, далее через Пролив Дэвиса и по побережью острова Гренландия до мыса Брустер, через Датский пролив до мыса Рейдинупюр на острове Ислfндия, по его побережью до мыса Герпир, затем к Фарерским островам, далее к Шетландским островам и по 61° северной широты до побережья Скандинавского полуострова[7]. Границей с Тихим океаном является линия в Беринговом проливе от мыса Дежнёва до мыса Принца Уэльского.
[править]Моря" Основой прямой призмы является равнобедренный треугольник с углом a при основании и радиусом вписанной окружности r. Диагональ боковой грани, проходящей через основание равнобедренного треугольника, наклонена к плоскости основания под углом y . Отметьте, какие из приведенных четырех утверждений правильные
1. Плоскость, проходящая через боковое ребро призмы и уентр круга, вписанного в основание, делит двугранный угол при боковом ребре призмы пополам
2. Боковое ребро призмы равна 2r*ctg*a/2*tgy
3. Одна из сторон основания призмы равна r*ctg*a/2
4. Один из двугранных углов при боковом ребре призмы равна a"
Объяснение:
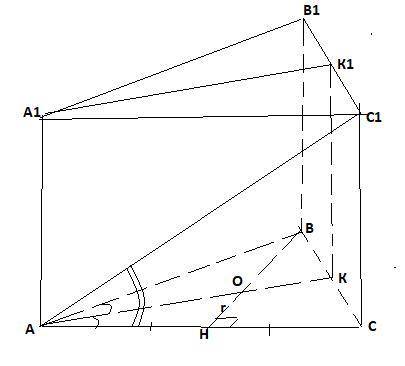
1) Т.к. центр вписанной окружности лежит в точке пересечения биссектрис, то плоскостью, проходящей через боковое ребро призмы и центр круга, вписанного в основание, будет плоскость АКК₁А₁ , где АК, А₁К₁-биссектрисы нижнего и верхнего оснований.
Поэтому 1 утверждение верное.
2) Боковое ребро найдем из ΔАСС₁ -прямоугольного : СС₁=АС*tgy.
АС найдем из ΔАОН :
ΔАВС-равнобедренный. В равнобедренном
треугольнике биссектриса ВН является высотой и
медианой .АК-биссектриса, значит ∠ОАН=α/2 .
АН= r /(tgα/2 ) , 2АН=АС= =2r*ctg α/2 .
Получаем СС₁=2r*ctg α/2 *tgy.
Поэтому 2 утверждение верное.
3) 3 утверждение неверное , т.к. в п 2 найдена сторона основания АС=2r*ctg α/2 . а боковая сторона будет искаться через косинус или синус ΔАВН.
4)4 утверждение верное . Это двугранный угол , например САА₁В, т.к
АА₁⊥АС и АА₁⊥АВ и ∠ВАС=α
Диагональ основания правильной четырехугольной пирамиды равна 10 см, а боковое ребро 13 см. Найти площадь диагонального сечения пирамиды.
Основанием правильной четырехугольной пирамиды является квадрат, а вершина пирамиды проецируется в его центр, т.е. точку пересечения его диагоналей. .
Следовательно, высота ЅО принадлежит диагональному сечению АЅС пирамиды.
Пусть дана пирамида SABCD, SO -её высота. Диагонали основания равны, точкой пересечения делятся пополам, а диагональные сечения - равные равнобедренные треугольники.
Высота ЅО перпендикулярна основанию и любой прямой, на плоскости АВСD. =>
∆ АОЅ - прямоугольный.
По т.Пифагора ЅО=√(SA²-AO²)=√(169-25)=12см
S(ASC)=SO•AC:2=12•5=60 см²