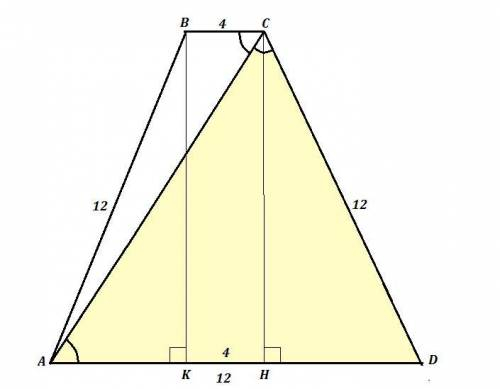
Окружность с центром в точке А( 5 ; 6 ) . Диаметр ВС , В( 3 ; 4 ) ,
С ( 7 ; 8 ) .
б) Построим ΔВСD , как показано на рисунке . ∠D=90° ,
∠CBD=∠BCD=45° ⇒ k = tg∠CBD = tg45° = 1 .
Если продлить прямую ВС , то она пересечёт ось ОУ в точке с ординатой, равной b=1 .
Получим уравнение прямой в виде y = kx + b такое : у = х+1 .
а) Из ΔBCD по теореме Пифагора найдём ВС .
ВС²=ВD²+CD²=4^2+4^2=16+16=32 , BC=√32 = 4√2
ВC - диаметр окружности ⇒ радиус равен половине диаметра ⇒
R=2√2=√8 .
Уравнение окружности имеет вид (x-5)² + (y-6)² = 8 .
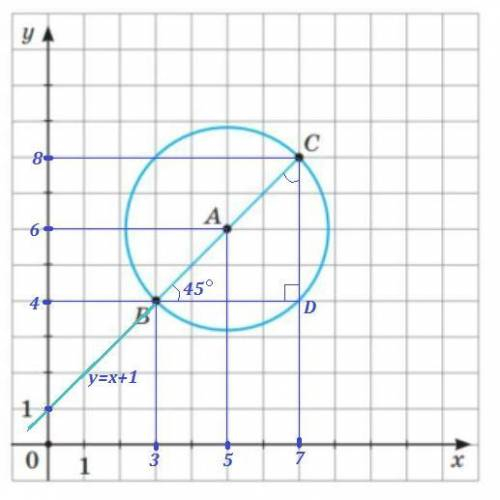
Трапеция АВCD - равнобокая, АВ=CD .
Основания АD=12 cм , BC=4 см .
АС - биссектриса ⇒ ∠АСВ=∠АСD .
Так как ВС || AD и АС - секущая , то ∠АСВ=∠САD как внутренние накрест лежащие углы .
Но по условию ∠АСВ=∠АСD , значит ∠САD=∠ACD и
ΔACD - равнобедренный , AD=CD=12 см . Тогда и АВ=CD=12 cм .
Опустим перпендикуляры из вершин В и С на АD , ВК⊥AD , CH⊥AD .
Тогда ВСНК - прямоугольник и ВС=КН=4 см .
ΔАВК = ΔCDH по гипотенузе (CD=AB) и острому углу (∠А=∠D как углы при основании равнобедренной трапеции) ⇒ АК=DH .
АК=DH=(AD-КН):2=(12-4):2=4 (см)
По теореме Пифагора найдём высоту трапеции из ΔCDH :
CD²=CH²+DH² ⇒ CH²=CD²-DH²=12²-4²144-16=128 ,
CH=√128=8√2 (см)
Площадь трапеции равна
S = (AD+BC):2*CH = (12+4):2*8√2 = 64√2 (см²)