Менелая
PK/KQ *QS/SN *NR/RP =1 <=> 2/3 *3/1 *NR/RP =1 <=> NR/RP= 1/2
PN/NR *RS/SK *KQ/QP =1 <=> 1/1 *RS/SK *3/5 =1 <=> RS/SK= 5/3
Чевы
PN/NR *RM/MQ *QK/KP =1 <=> 1/1 *RM/MQ *3/2 =1 <=> RM/MQ= 2/3
Менелая
QK/KP *PS/SM *MR/RQ =1 <=> 3/2 *PS/SM *2/5 =1 <=> PS/SM= 5/3
RS/SK *KL/LN *NP/PR =1 <=> 5/3 *KL/LN *1/2 =1 <=> KL/LN= 6/5
RN/NP *PL/LS *SK/KR =1 <=> 1/1 *PL/LS *3/8 =1 <=> PL/LS= 8/3
PL/PM =PL/PS *PS/PM =8/11 *5/8 =5/11
PL/LM= 5/6
Разумеется, после того, как установлено, что QN - медиана, можно сразу сказать, что
RM/MQ =PK/KQ =2/3 (PR||KM)
PL/ML =LN/LK (PLN~MLK)
PS/MS= SR/SK (PSR~MSK)
1) Отразим рисунок относительно прямой AB, окружности перейдут сами в себя, а K – перейдёт в точку K', симметричную относительно прямой AB. Если K не лежит на AB, то K и K' не совпадают, и K' – тоже точка касания, чего быть не может.
2) Радиусы, проведённые в точку касания, перпендикулярны касательной, поэтому AN и BM перпендикулярны NM, а тогда параллельны, ANMB – прямоугольная трапеция.
Проведём высоту трапеции AD. ANMD – прямоугольник, поэтому MD = AN = r, тогда BD = 2r. Кроме того, AB = AK + KB = 4r, поэтому ∠DAB = 30° (противолежащий катет равен половине гипотенузы), а по теореме Пифагора .
.
Площадь трапеции ANMB равна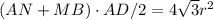
Площадь сектора KAN с центральным углом 90° + 30° = 120° = π/3 равна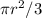
Площадь сектора KBM с центральным углом 90° - 30° = 60° = π/6 равна
Площадь искомой фигуры