Объяснение:
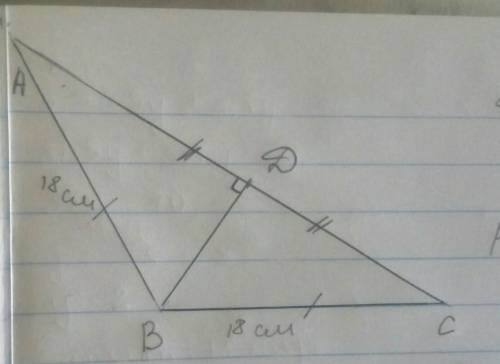
1) Т.к. АВ=ВС, то треугольник АВС-р/б, следовательно, ВD - медиана, биссектриса, высота.
Т.к. ВD - биссектриса, то в треугольнике АВD угол АВD= 120°:2=60°
Т.к. ВD - высота, то в треугольнике АВD угол АDВ = 90°
Сумма углов треугольника равна 180°, следовательно, угол ВАD = 180°-(60°+90°)=180°-150°=30°.
2) Мы узнали, что угол ВАD=30°, найдём длину ВD.
Треугольник АВD - прямоугольный.
В прямоугольном треугольнике катет, лежащий напротив угла в 30° равен половине гипотенузы.
Угол ВАD = 30°, угол ВАD лежит напротив ВD, следовательно ВD = 0,5АВ=0,5×18=9 (см).
ответ: 1) 60°, 90°, 30°.
2) 9 см.
Вот чертёж, дано, надеюсь, напишешь.
1. Пусть х - один из вертикальных углов, тогда угол, смежный с ним 180° - х, так как сумма смежных углов равна 180°.
Вертикальные углы равны, тогда 2х - сумма двух вертикальных углов.
Получаем уравнение:
2x + 30° = 180° - x
3x = 150°
x = 50°
ответ: каждый из двух вертикальных углов равен 50°.
2. Пусть х - один из углов, тогда угол, смежный с ним 180° - х, так как сумма смежных углов равна 180°.
Получаем уравнение:
1/8 x + 3/4 (180° - x) = 90° |· 8
x + 6 (180° - x) = 720°
x + 1080° - 6x = 720°
5x = 360°
x = 72° - один из смежных углов.
180° - 72° = 108° - второй угол.
Разность данных углов:
108° - 72° = 36°
ответ: 36°.
3. ∠1 + ∠2 + ∠3 - ∠4 = 280° по условию задачи.
∠1 = ∠3 и ∠2 = ∠4 как вертикальные, значит
2 · ∠1 = 280°
∠1 = 140°
∠3 = ∠1 = 140°
∠2 = 180° - ∠1 = 180° - 140° = 40°, так как ∠2 и ∠1 смежные, а сумма смежных углов равна 180°.
∠4 = ∠2 = 40°
ответ: 40°, 40°, 140°, 140°.

у прямоугольника углы при основании равны, следовательно ОВС=ОСВ=130/2=65 градусов, а так как С=90 градусов, то АСД=90-65=25 градусов