Сечения шара двумя параллельными плоскостями, между которыми лежит центр шара, имеют площади 144π см, 25π см. Найти площадь поверхности шара, если расстояние между параллельными плоскостями равен 17 см
* * *
Сечение шара плоскостью - круг.
Расстояние между плоскостями равно длине перпендикуляра, опущенного с одной плоскости на другую.
Центр шара и центры сечений параллельными плоскостями лежат на одной прямой.
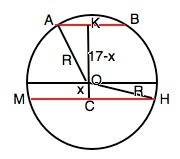
На схематическом рисунке приложения – сечение шара через его центр О и центры сечений.
АК- радиус меньшего сечения, СН - радиус большего сечения, СК - расстояние между центрами сечений, ОА=ОН - радиус шара.
Квадрат радиуса меньшего сечения АК²=S1:π=25
Квадрат радиуса большего сечения СН²=S2:π=144
Обозначим расстояние между центром шара и большим сечением СО=х, тогда между центром шара и меньшим сечением ОК=17-х.
Из ∆ АОК по т.Пифагора
R²=АК²+ОК²
Из СОН
R²=CH²+CO²
Приравняем оба значения R²:
АК²+ОК²=CH²+CO²
25+289-34х+х²=144+х*
34х=170
х=5
R²=ОН²=25+144=169
Формула площади поверхности шара
S=4πR²
S=4π•169=676π см²
Ну, смотри. Задача на самом деле легкая) Нам дан равносторонний треугольник - значит, что уже можно выделить несколько условий. Главное - очевидно, что все его стороны равны. По правилу, биссектриса равностороннего треугольника=его медиане=его высоте,=> ВК не только биссектриса, но и высота, и медиана, т. е., делит сторону АС пополам. АК=КС, АВ=ВС. И тут же нам дано, что АК+ВС=27. Как мы уже выяснили, АК=КС, а ВС=АВ, значит, сумма АК+ВС=КС+АВ. А тут уж все очень просто: вот и весь периметр. Итак, Р=(АК+ВС) + (КС+АВ)=АК+ВС+КС+АВ=27+27=54 (см).
ответ: Р(АВС)=54 см.
P. S. и на будущее: с рисунком в геометрии, как нас учили, гораздо проще, а главное, что задача уже наполовину сделана)
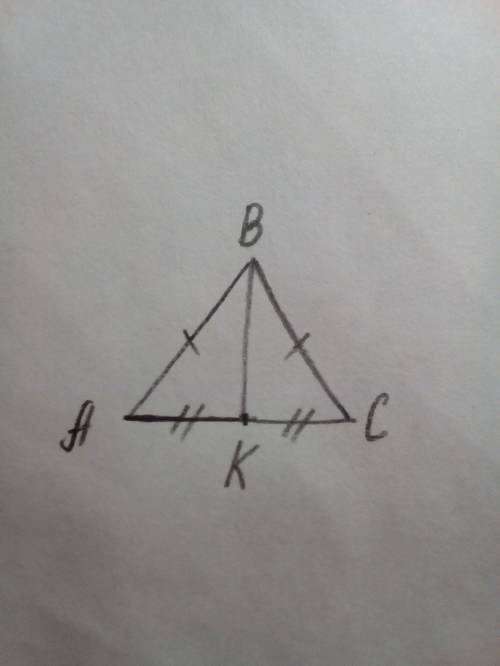
С=((Ха+Хв)/2; (Уа+Ув)/2;(Zа+Zв)/2), где X,Y,Z (а,в) - координаты концов отрезка.