Тема: "окружающая среда"
* * * для удобства плоскость (ABCD) обозначаем через Ψ * * *
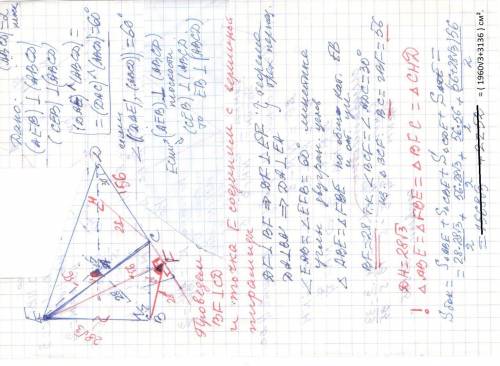
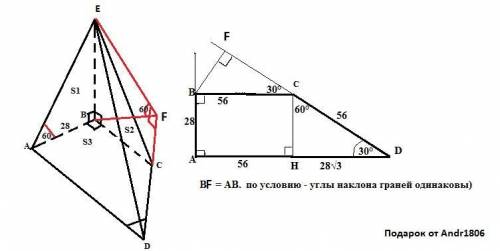
EABCD - пирамида , основание которой трапеция ABCD ;
AD || BC ; AB =28 ; ∠A =∠B =90° ; ∠D =30° ; | [AB] < [CD] ; [BC] < [AD]
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ; ∠ ( (CDE) , Ψ ) =∠ ( (ADE) , Ψ ) = 60°
--------------------------
1. Трапеция ABCD ПРЯМОУГОЛЬНАЯ
- - -
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ⇒ EB ⊥ Ψ
DA⊥ BA ⇒DA ⊥ EA ; ∠EAB =60° линейный угол двугранного угла
EADC ; Построим линейный угол двугранного угла EDCA
Проведем BF ⊥ CD и основание F этого перпендикуляра соединим с вершиной ПИРАМИДЫ E. Получаем ∠EFB = 60° линейный угол двугранного угла EDCA .
* * * ! ΔABE = ΔFBE =Δ BFC = ΔCHD учитывая ∠D =∠BCF =30° * * *
Вычисление площадей боковых граней и т.д. cм приложение
диаметры относятся так же, как и радиусы...
d/D = (2r) / (2R) = r/R
т.е. нужно доказать, что r/R = a/b
радиусы, проведенные в точку касания _|_ касательной --->
получили два подобных прямоугольных треугольника (в них острые углы вертикальны, т.е. равны...)))
осталось записать отношение соответственных сторон...
гипотенузы относятся как катеты, лежащие против равных (вертикальных)) углов...