Здесь следует рассмотреть сечение шара плоскостью, которая делит и шар,и конус таким образом, что все мы наблюдаем как бы в срезе. Смотри рисунок. Используем расширенную теорему синусов, чтобы узнать радиус описанной окружности вокруг треугольника АВС. Заметим, что этот треугольник равнобедренный. АВравно ВС как образующие конуса. Найдем АВ по теореме Пифагора
AB^2=AH^2+HB^2
AB^2=(3sqrt3)^2+3^2
AB^2=27+9
AB^2=36
AB=6 см.
Найдем противолежащий угол ВСА. Он равен углу ВАС.
По теореме синусов нам нужен синус этого угла.
sinangle BAC=frac{BH}{AB}
sinangle BAC=frac{3}{6}
sinangle BAC=frac{1}{2}
По теореме синусов
2R=frac{AB}{sinangle BCA}
2R=frac{6}{sinangle BAC}
2R=frac{6}{0,5}
2R=12
R=6 - радиус описанной окружности вокруг треугольника АВС, и радиус шара описанного вокруг конуса одновременно.
Объем шара находится по стандартной формуле
V=frac{4}{3}pi*R^3
V=frac{4}{3}pi*6^3
V=4pi*6^2*2
V=8pi*36
V=288pi
Объяснение:
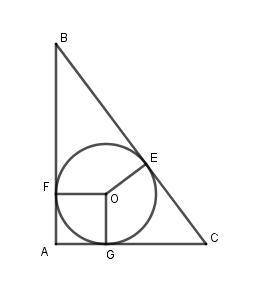
EC = GC = 5 см, BE = BF = 7.5 см. Пусть AF = AG = x, тогда
AB = AF + BF = x + 7.5 см
AC = AG + GC = x + 5 см
BC = BE + CE = 7.5 + 5 = 12.5 см
По т. Пифагора:
(x+7.5)² + (x+5)² = 12.5²
(x+7.5)² - 12.5² + (x+5)² = 0
(x+7.5+12.5)(x+7.5-12.5) + (x+5)² = 0
(x+20)(x-5) + (x+5)² = 0
x² - 5x + 20x - 100 + x² + 10x + 25 = 0
2x² + 25x - 75 = 0
D = 625 + 600 = 1225
x₁ = (-25 + 35)/4 = 2.5 см
x₂ = (-25-35)/4 < 0 - не подходит.
Имеем: AB = 2.5 + 7.5 = 10 см, AC = 2.5 + 5 = 7.5 см.
P = 12.5 + 10 + 7.5 = 30 см
S = AB*AC/2 = 10*7.5/2 = 37.5 см²