извините что то не могу добавить рисунок! треугольники ВОС и АОД подобны где точка о пересечения диагоналей трапеций и кэоффициент подобия равен 34/36 = 17/18 , так как по условию трапеция прямоугольная по тоеоме пифагора обозначим АО за х тогда ОС = 17/18 *х
как известно Высота прямоугольного треугольника -среднее геометрическое между проекциями катетов на гипотенузу,
34^2=x*17/18 *x
x=6√34
значит другая диагональ равна 6√34+6√34*17/18, теперь сами основания
по теореме пифагора нижнее равна
(6√34)^2 +36^2 =√2520
верхнее
34^2+ (6√34*17/18)^2 ~ 2247
что то диагональ какие то может неправильно написали!
Определите косинус угла между треугольником A B1C и плоскостью основания куба ABCDA1B1C1D1 со стороной 1.
Объяснение:
Нужно найти двугранный угол В₁АСВ.
В кубе все грани квадраты. Диагональ квадрата равна √(1²+1²)=√2 , половина диагонали 0,5√2. Пусть О-точка пересечения диагоналей основания.
Диагонали квадрата взаимно перпендикулярны , значит ОВ⊥АС. Тк. проекция ОВ⊥АС ,прямой лежащей в плоскости , то и наклонная В₁О⊥АС. Поэтому ∠В₁ОВ-линейный угол двугранного В₁АСВ.
ΔВВ₁О- прямоугольный , tg∠В₁ОВ=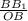
, tg∠В₁ОВ= 
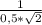=√2.
1+tg²∠В₁ОВ=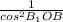
, 1+√2²= 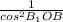,cos∠B₁OB=
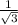, cos∠B₁OB=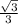
r=8/2√3=4√3
2) Суммы сторон четырехугольника, описанного около окружности , равны.
7+11=х+2х
3х=18
х=6
BC= 6, то AD=12