Дан треугольник abc: сd-биссектриса угла с, bm-бис-са угла b, сd пересекается с bm в т.о, со/оd=26/1, ав=7, с лежит на ав, м лежит на ас. найти: периметр треуг-ка. нужно решение!

👇

Ответ:

yaya4

14.03.2021

Биссектриса угла делит сторону на части, пропорциональные прилежащим сторонам.
В тр-ке DBC BO - биссектриса. Значит, CO/OD=BC/BD=26/1. Пусть 1ч=x. Тогда, BD=x, BC=26x. AD=7-x. В тр-ке ABC CD - биссектриса. Значит, AC/BC=AD/DB. Тогда
AC=BC*AD/BD. AC=26x*(7-x)/x=26*7-26x=182-26x.
Pabc=AC+AB+BC=182-26x+7+26x=189

4,8(73 оценок)

Открыть все ответы

Ответ:

Милаякрасавица

14.03.2021

А₁А₂ = 2 см

Объяснение:

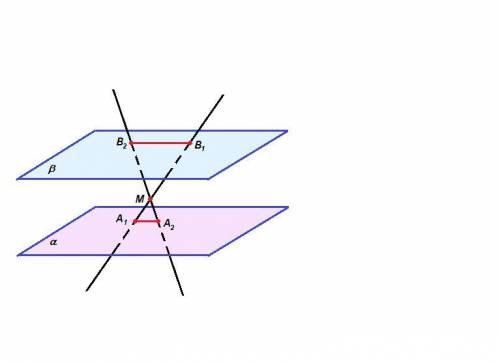
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.

Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит

А₁А₂ ║ В₁В₂.

Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,

∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит

ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.

МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см

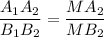
$\dfrac{A_{1}A_{2}}{B_{1}B_{2}}=\dfrac{MA_{2}}{MB_{2}}$

Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,

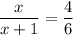
$\dfrac{x}{x+1}=\dfrac{4}{6}$

6x = 4(x + 1)

6x = 4x + 4

2x = 4

x = 2

А₁А₂ = 2 см

Умоляю,! площини а і в паралельні. через точку м що знаходиться між цими площинами проведено дві пря

4,6(50 оценок)

Ответ:

nikols7

14.03.2021

Оболочка, являясь целостной, неоднородна на разных широтах, на суше и в океане. неравномерному поступлению солнечного тепла на земную поверхность оболочка разнообразна. близ экватора, например, где много тепла и влаги, природа отличается богатством живых организмов, более быстро проходящими природными процессами, в полярных областях, наоборот, медленно текущими процессами и бедностью жизни. на одних и тех же широтах природа также может быть различной. это зависит от рельефа и удаленности от океана. поэтому оболочку можно разделить на разные по размерам участки, территории или природно-территориальные комплексы (сокращенно природные комплексы, или пк). формирование любого природного комплекса происходило длительное время. на суше оно осуществлялось под влиянием взаимодействия компонентов природы: горных пород, климата, воздушных масс, воды, растений, животных, почв. все компоненты в природном комплексе, как и в оболочке, переплетены друг с другом и образуют целостный природный комплекс, в нем также происходит обмен веществ и энергии. природным комплексом называется участок земной поверхности, который отличается особенностями природных компонентов, находящихся в сложном взаимодействии. каждый природный комплекс имеет более или менее четко выраженные границы, обладает природным единством, проявляющимся в его внешнем облике (например, лес, болото, горный массив, озеро и т. природные комплексы океана, в отличие от суши, состоят из следующих компонентов: воды с растворенными в ней газами, растений и животных, горных пород и рельефа дна. в мировом океане выделяются крупные природные комплексы - отдельные океаны, менее крупные - моря, заливы, проливы и пр. кроме того, в океане различают природные комплексы поверхностных слоев воды, различных толщ воды и океанического дна. природные комплексы бывают разных размеров. отличаются: они и по образованию. большие природные комплексы - это материки и океаны. образование их обусловлено строением земной коры. на материках и океанах выделяют менее крупные комплексы - части материков и океанов. в зависимости от количества солнечного тепла, т. е. от широты, бывают природные комплексы экваториальных лесов, тропических пустынь, тайги и т. д. примерами мелких могут служить, например, овраг, озеро, речная долина, морской залив. а самый большой природный комплекс земли - оболочка. все природные комплексы испытывают на себе огромное влияние человека. многие из них уже сильно изменены многовековой деятельностью человечества. человек создал новые природные комплексы: поля, сады, города, парки и др. такие природные комплексы называются антропогенными (от греч. «антропос» - человек).\

4,8(48 оценок)

Это интересно:

Кулинария-и-гостеприимство

16.04.2020

Морские водоросли: как приготовить их правильно...

Стиль-и-уход-за-собой

31.05.2021

Как правильно делать макияж: советы для начинающих...

Образование-и-коммуникации

23.06.2020

7 простых шагов, как полюбить чтение...

05.07.2020