Обозначим вершины треугольника А, В, С, причем АВ=ВС.
Т.к. ∆ АВС - равнобедренный, высота ВН, проведенная к основанию, является медианой, и, следовательно, ВН - срединный перпендикуляр. Точка пересечения срединных перпендикуляров треугольника - центр описанной вокруг него окружности.
Расстояние от О до вершин А, В и С равно радиусу. R=ВО=СО=17 см.
∆ СОН - прямоугольный, его гипотенуза и один из катетов - из Пифагоровых троек ( 8, 15,17), ⇒, НС=15 см ( проверьте по т.Пифагора).
Отсюда АС=2•15=30 см
По т.Пифагора AB=ВС=√(BH*+CH*)=√(625+225)=√850=5√34 см
Р=30+2•5√34=10•(3+√34) см
S=BH•CH=375 см²
10 см.
Объяснение:
Искомое расстояние - средняя линия трапеции с основаниями, рваными 12см и 8см. Найдем по формуле: (12+8)/2 =10см.
Или так:
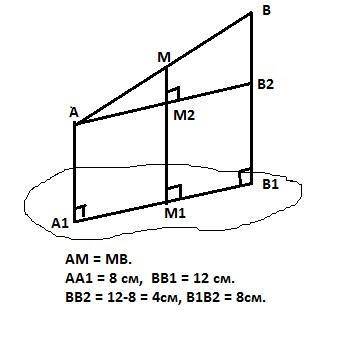
Пусть отрезок АВ, концы отрезка проецируются на плоскость в точки А1 и В1 соответственно. АА1 = 8см,
ВВ1 = 12см. Фигура АВВ1А1 лежит в одной плоскости, пересекающей данную по прямой А1В1.
Проведем прямую АА2 параллельно А1В1. Тогда в прямоугольном треугольнике АВА2 катет ВА2 равен
ВА2 = 12 - 8 = 4 см.
Средняя линия ММ2 этого треугольника равна 2см.
Тогда расстояние от середины отрезка АВ до плоскости равно
ММ1 = ММ2 + М2М1 = 2 + 8 =10см.
Тогда ВМ / ВК = cos МВК. Угол МВК = arc cos (ВМ / ВК).
Угол СВК = КВА = 45°, так как ВК - биссектриса прямого угла.
Угол СВМ = 45 - (arc cos (ВМ / ВК)),
а угол МВА =45 + (arc cos (ВМ / ВК)).
Отсюда стороны треугольника равны:
ВС = ВМ / cos(45 - (arc cos (ВМ / ВК))).
BA = BM / cos(45 + (arc cos (ВМ / ВК)).
Гипотенузу АС находим по Пифагору: СА = √(ВС²+ВА²), тогда площадь треугольника АВС = (1/2)*АС*ВМ.