Основи трапеції дорівнюють 15 см і 36 см, а бічні сторони – 13 см і 20 см. знайти площу даної трапеції.

👇

Увидеть ответ

Ответ:

Mimiminika

13.03.2021

Пусть BC=15 см; AD=36 см; АВ=13 см ; CD=20 см.

Проводим ВК || CD

BK=CD=20 см

BC=KD=15 см

AK=AD-KD=36-15=21 см

Получаем треугольник АВК и параллелограмм ВСКD.

Площадь треугольника АВК находим по формуле Герона

$S=\sqrt{p\cdot(p-a)\cdot(p-b)\cdot(p-c)}\\ \\ p=\frac{a+b+c}{2}$

p=(AB+BC+AK)/2=27 cм

S=√(27·(27-13)·(27-20)·(27-21))=126 кв. м

C другой стороны

S ( Δ АВК)= (1/2)AK*BH

BH=12

ВН - высота треугольника АВК а значит и трапеции ABCD.

S_(трапеции)=(AD+BC)·BH/2=306 кв. м

Основи трапеції дорівнюють 15 см і 36 см, а бічні сторони – 13 см і 20 см. знайти площу даної трапец

4,5(21 оценок)

Открыть все ответы

Ответ:

zuste

13.03.2021

Украинский:

трикутник АВС, кут = 90, ВС - гіпотенуза, АН-висота на ВС, ВН = 28, СН = 7

ВН / АН = АН / НС. 28 / АН = АН / 7, АН в квадраті = 196, АН = 14

АС = корінь (АН в квадраті + НС в квадраті) = корінь (196 + 49) = корень245 = 7 х корень5

АВ = корінь (АН в квадраті + ВН в квадраті) = корінь (196 + 784) = корень980 =

= 14 х корень5

Площа = 1/2 х АС х АВ = 1/2 х 7 х корень5 х 14 х корень5 = 245

Русский:

треугольник АВс, уголА=90, ВС - гипотенуза, АН-высота на ВС, ВН=28, СН=7

ВН/АН=АН/НС. 28/АН=АН/7, АН в квадрате = 196, АН=14

АС = корень(АН в квадрате + НС в квадрате) = корень(196 + 49) =корень245 =7 х корень5

АВ = корень (АН в квадрате + ВН в квадрате) = корень(196 + 784) = корень980 =

=14 х корень5

Площадь = 1/2 х АС х АВ = 1/2 х 7 х корень5 х 14 х корень5 = 245

4,4(68 оценок)

Ответ:

DarkOP

13.03.2021

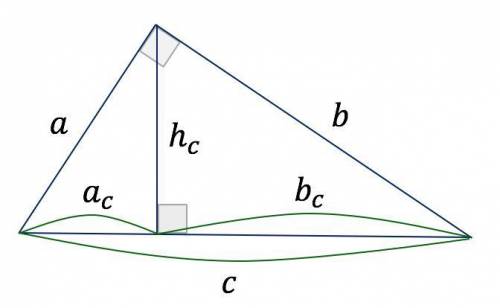
Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.

Перший б

Катет прямокутного трикутника — середнє пропорційне між гіпотенузою і проекцією цього катета на гіпотенузу:

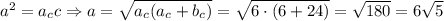$a^{2} = a_{c}c \Rightarrow a = \sqrt{a_{c}(a_{c}+ b_{c})} = \sqrt{6 \cdot (6 + 24)} = \sqrt{180} = 6\sqrt{5}$ см

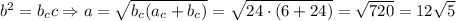$b^{2} = b_{c}c \Rightarrow a = \sqrt{b_{c}(a_{c}+ b_{c})} = \sqrt{24 \cdot (6 + 24)} = \sqrt{720} = 12\sqrt{5}$ см

Площа 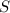прямокутного трикутника знаходится як півдобуток його катетів:

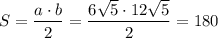$S = \dfrac{a \cdot b}{2} = \dfrac{6\sqrt{5} \cdot 12\sqrt{5}}{2} = 180$ см²

Другий б

Висота 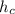$h_{c}$ прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:

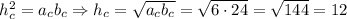$h^{2}_{c} = a_{c}b_{c} \Rightarrow h_{c} = \sqrt{a_{c}b_{c}} = \sqrt{6 \cdot 24} = \sqrt{144} = 12$ см

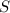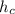Площа будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти $h_{c}$ , що до неї проведена:

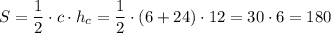$S = \dfrac{1}{2} \cdot c \cdot h_{c} = \dfrac{1}{2} \cdot (6 + 24) \cdot 12 = 30 \cdot 6 = 180$ см²