1) Есть треугольник MKP
Есть треугольник MKPпроведём высоту из вершины К на МР, получим точку Н, она будет лежать на середине МР, т.к. треугольник равнобедренный
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^2
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100НК^2 = 100 - 36
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100НК^2 = 100 - 36НК^2 = 64
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100НК^2 = 100 - 36НК^2 = 64НК = 8
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100НК^2 = 100 - 36НК^2 = 64НК = 8теперь получили прямоугольный треугольник NKH, где NK = 15, KH = 8, по теореме пифагора получаем
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100НК^2 = 100 - 36НК^2 = 64НК = 8теперь получили прямоугольный треугольник NKH, где NK = 15, KH = 8, по теореме пифагора получаемNK^2 + KH^2 = NH^2
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100НК^2 = 100 - 36НК^2 = 64НК = 8теперь получили прямоугольный треугольник NKH, где NK = 15, KH = 8, по теореме пифагора получаемNK^2 + KH^2 = NH^2255 + 64 = NH^2
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100НК^2 = 100 - 36НК^2 = 64НК = 8теперь получили прямоугольный треугольник NKH, где NK = 15, KH = 8, по теореме пифагора получаемNK^2 + KH^2 = NH^2255 + 64 = NH^2319 = NH^2
она будет лежать на середине МР, т.к. треугольник равнобедренныйпо теореме пифагора получаем:МН^2 + НК^2 = МК^236 + НК^2 = 100НК^2 = 100 - 36НК^2 = 64НК = 8теперь получили прямоугольный треугольник NKH, где NK = 15, KH = 8, по теореме пифагора получаемNK^2 + KH^2 = NH^2255 + 64 = NH^2319 = NH^2NH = sqrt(319)
Данная пирамида не существует.
Объяснение:
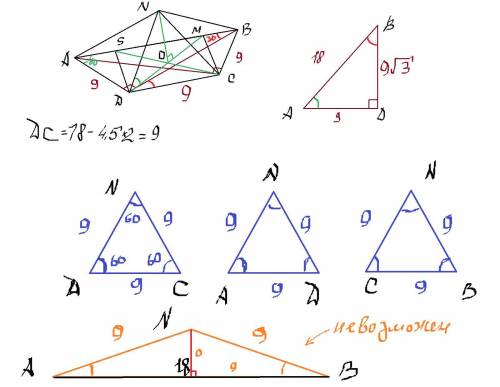
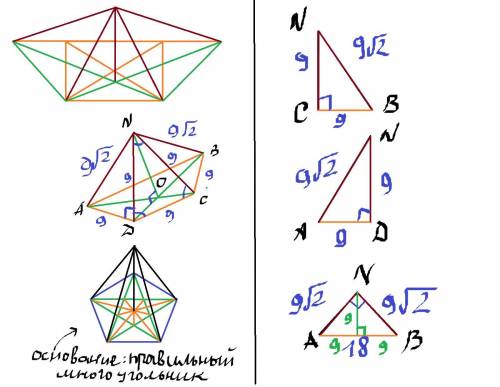
Дано условие: Каждое боковое ребро пирамиды должно образовывать с плоскостью основания угол 60°. Такое условие возможно только при условии, что в основании лежит правильный многоугольник - многоугольник, у которого равны все стороны и все углы. Поскольку равнобокая трапеция не является правильным многоугольником, можно сказать, что данная пирамида невозможна. Однако, если представить, что лишь 2 боковых ребрa образуют с плоскостью основания угол 60°, то задача станет вполне решаемой.
Итак, представим пирамиду NABCD, где NO - h - , ∠NDC=∠NCD=60°, ∠ADB=90°, ∠BAD=90°. Из ΔАВD по частному случаю прямоугольных треугольников (30°, 60°, 90°):
AD=9, AB=18, BD=9√3; => DC = 18 - 4,5 - 4,5 = 9
Так как, по условию, ΔNDC - равносторонний, стороны ND= DC= NC= 9.
Исходя из теоремы о трёх перпендикулярах, получаем, что ∠ADC = ∠NCB = 90° (∠ADB= ∠ACB= 90°, ∠NOD= ∠NOC= 90°.
Из прямоугольных равнобедренных треугольников ΔNAD & ΔNBC, по частному случаю прямоугольных треугольников (45°, 45°, 90°):
NB = AN = 9√2
ответ: Боковые рёбра пирамиды, в основании которой лежит равнобокая трапеция, при условии, что ЛИШЬ 2 БОКОВЫХ РЕБРА ND и DC образуют с плоскостью основания угол 60°:
NA= NB = 9√2, ND= DC = 9.
тогда вторая сторона 0,5х см;
третья сторона х+3,2 см;
х+0,5х+х+3,2=9,8;
2,5х=9,8-3,2;
х=6,6:2,5=2,64 см одна сторона;
0,5*2,64=1,32 см вторая сторона;
2,64+3,2=5,84 см третья сторона;
обращаем внимание на то, что сумма двух сторон треугольника меньше третьей стороны
2,64+1,32<5,84;
треугольника с такими сторонами не существует;