ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
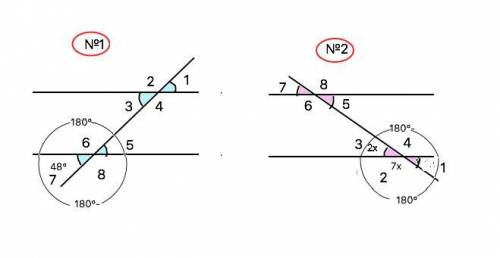
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
АВ, ВС - боковые стороны, АС - основание, ВО - высота
S треугольника АВС = (16·АС)/2.
По другой формуле S треугольника АВС = (АВ·ВС·АС)/4R. Не забывая, что АВ=ВС, приравниваем эти формулы и получаем: 8АС=(АВ²·АС)/40. Отсюда 320=АВ², АВ=8√5. По теореме Пифагора в треугольнике АВО АО=√АВ²-ВО²=√320-256=√64=8. Следовательно, АС=2·8=16, S=(16·16)/2=128