Итак,
Для решения нам нужно знать 3 признака подобия треугольников:
1)по двум пропорциональным сторонам и углу между ними
2)по двум углам
3)по трём пропорциональным сторонам
1) ΔCDO~ΔABO
Доказательство:
∠COD=∠AOB(вертикальные углы)
∠DCO=∠OBA(накрест лежащие углы при параллельных прямых а и б)
Выполняется второй признак подобия треуг. по двум углам
Ч.Т.Д
2)ΔFLK~ΔFMN
Доказательство:
∠F-общий
∠FKL=∠FMN(прямые углы)
Выполняется второй признак подобия треуг. по двум углам
Ч.Т.Д
3) ΔMHK~ΔMCD
Доказательство:
M-общий угол
∠MHK=∠MCD(соответственные углы при параллельных прямых)
Выполняется второй признак подобия треуг. по двум углам
Ч.Т.Д
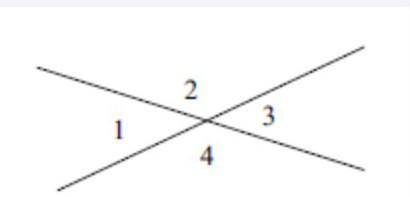
Решение, а) По условию Z2 + Z4 = 220°. Эти углы вертикальные, поэтому Z2 = Z4 = 110°.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°, откуда Z1 = 180° -- 110° = 70°.
Углы 3 и 1 вертикальные, поэтому Z3 = Z1 = 70°.
б) Углы 1 и 3, а также 2 и 4 вертикальные, поэтому Z3 = Zl, Z4 = = Z2. Подставив эти выражения в данное равенство, получим:
3(2Z1) = 2Z2,
или
3Z1 =Z2.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°. Из этих двух равенств находим Z1 и Z2: Z1 = 45°, Z2 = 135°.
Z3 = Z1, поэтому Z3 = 45°; Z4 = Z2, поэтому Z4 = 135°
в) По условию Z2 — Z1 = 30°. Эти углы смежные, следовательно, Zl + Z2 = 180°. Из этих двух равенств имеем: Z1 = 75°, Z2 = 105°.
Z3 = Z1, поэтому Z3 = 75°; Z4 = Z2, поэтому Z4 = 105°.
ответ, a) Zl = Z3 = 70°, Z2 = Z4 = 110°; б) Zl =Z3 = 45°, Z2 = = Z4 = 135°; в) Zl = Z3 = 75°, Z2 = Z4 = 105°.
B1D=корень(AB²+AD²+AA1²)=корень(16+16+4)=6