Объяснение:
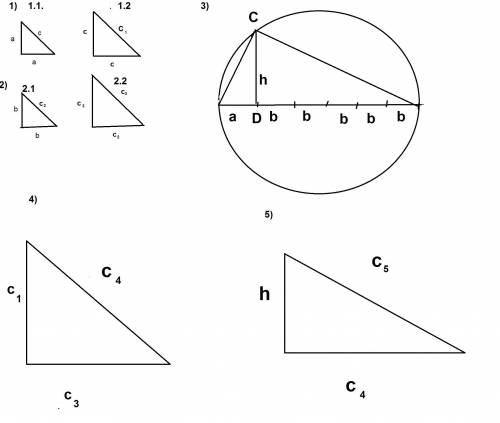
1) построение отрезка квадрат которого =4a²
1.1. Строим равнобедренный прямоугольный треугольник с катетами =a
обозначим гипотенузу с
По теореме Пифагора c²=a²+a²=2a²
1.2 Строим равнобедренный прямоугольный треугольник с катетами =с
обозначим гипотенузу с₁
По теореме Пифагора c₁²=с²+с²=2a²+2a²=4a²
2) аналогично пункту 1) строим отрезок квадрат которого =4b²
2.1. Строим равнобедренный прямоугольный треугольник с катетами =b
обозначим гипотенузу с₂
По теореме Пифагора c₂²=b²+b²=b²
2.2 Строим равнобедренный прямоугольный треугольник с катетами =с
обозначим гипотенузу с₃
По теореме Пифагора c₃²=с₂²+с₂²=2b²+2b²=4b²
3) построение отрезка квадрат которого = 5ab
Строим окружность диаметром a+5b
на диаметре откладываем отрезки a и 5b
обозначим точку которая делит диаметр на отрезки а и 5b D
через точку D проводим перпендикуляр до пересечения с оркужностью в точке С получаем прямоугольный треугольник в котором отрезок CD - высота обозначим ее как h
так как высота является средникм геометрическим проекций катетов то h=√(5ab) и h²=5ab
4) строим прямоугольный треугольник с катетами с₁ и с₃
обозначим его гипотенузу с₄
по теореме Пифагора с₄²=с₁²+с₃²=4a²+4b²
5) строим прямоугольный треугольник с катетами с₄ и h
обозначим его гипотенузу с₅
по теореме Пифагора с₅²=с₄²+h²=4a²+4b²+5ab=4a²+5ab+4b²
c₅= √(4a²+5ab+4b²)
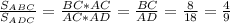
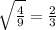 .
. 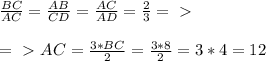
Поэтому, если диагональ основания - квадрата - равна 8√2 см, сторона основания равна 8 см.
Так как двугранный угол при основании равен 60°, сечение пирамиды, содержащее высоту - правильный треугольник.
Отсюда апофема каждой грани равна длине стороны основания.
Апофема=8 см.
Площадь полной поверхности - сумма площади основания и площади всех четырех граней.
S осн=a²
S бок=4*а*h:2
S бок=4*8*8:2=128 см²
S осн=8*8=64 см
S полн=128+64=192 см²