Сперва найдем вектора AB и CD
обозначу их через a и b
a=AB=(-1-3;5-2)=(-4;3)
b=CD=(-3-2;4-0)=(-5;4)
теперь 2a и 3b
2a=2*(-4;3)=(-8;6)
-3b=-3*(-8;6)=(24;-18)
терь р=(-8-24;6-(-18))=(-32;24)
110°
Объяснение:
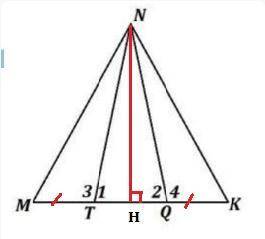
1) NH - медиана ΔTNQ ⇒ по свойству медианы TH=HQ.
По условию MT=QK ⇒ МH=HK, т.к. сумма равных отрезков даёт в итоге равные отрезки: MT+TH = QK+HQ. ⇒ NH - медиана ΔMNK.
По условию задачи NH - высота ΔMNK.
Если в треугольнике медиана и высота, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный.⇒ ΔMNK - равнобедренный, что и требовалось доказать.
ΔTNQ также равнобедренный, т.к. NH - медиана и высота.
2) ∠2 + ∠1 − ∠4 = 30°
∠2=∠1, т.к. у равнобедренного ΔTNQ углы при основании равны.
По свойству смежных углов: ∠4 = 180°-∠2 , но ∠2=∠1, поэтому ∠4=180°-∠1
⇒ ∠1+∠1-(180°-∠1)=30°
3*∠1=30°+180°
3*∠1=210°
∠1=70°
По свойству смежных углов: ∠3=180°-∠1=180°-70°=110°
вектор AB имеет координаты:(-4;3)(из координаты точки B вычитаем координаты точки A)
DC(5;-4)
Координаты вектора 2AB(-8;6)(Просто умножаем координаты AB на 2)
3DC(15;-12)
А теперь вычтем из 2AB 3DC
p(-23;18)