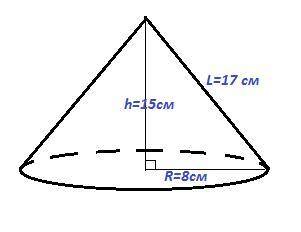
Площадь полной поверхности конуса равна 200π см, а его образующая - 17 см. Найдите объём конуса.
Полная поверхность конуса состоит из площади боковой поверхности и площади основания.
S = Sб + S₀ = πRL + πR² , где R - радиус основания, L - образующая
200π = πR · 17 + πR² | : π
R² + 17R - 200 = 0
D = 17² + 4 · 200 = 1089 = 33²
R₁ = (-17 + 33) : 2 = 8 см
R₂ = (-17 - 33) : 2 = -25 - не подходит по условию
Высота h, радиус основания R и образующая конуса L - это прямоугольный треугольник. Теорема Пифагора
h² = L² - R² = 17² - 8² = (17 - 8)(17 + 8) = 9·25
h = √(9·25) = 3·5 = 15 см
Объём конуса
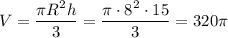 см³
см³
ответ: 320π см³
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы. Следовательно, чтобы центр описанной окружности лежал на АС, сторона АС должна быть гипотенузой треугольника, т.е она должна лежать против угла 90 градусов, противолежащий угол АВС, равен 80 град, следовательно центр окружности не лежит на АС