Сечение - правильный шестиугольник.
Объяснение:
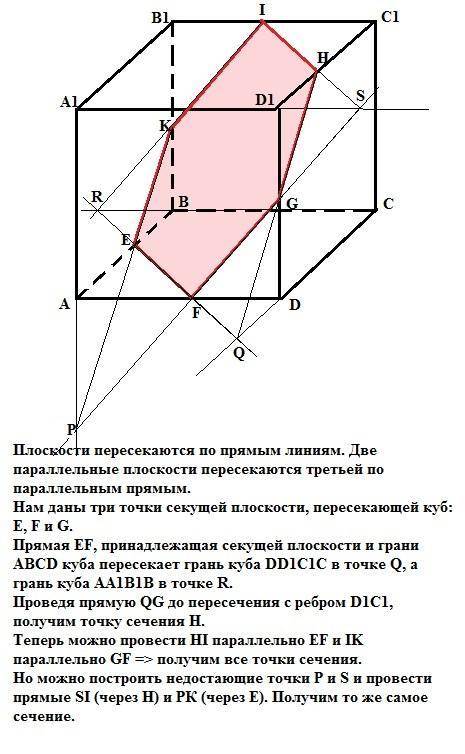
Плоскости пересекаются по прямым линиям. Две параллельные плоскости пересекаются третьей по параллельным прямым.
Нам даны три точки секущей плоскости, пересекающей куб: E, F и G, расположенные на ребрах АВ, AD и DD1 соответственно.
Прямая EF, принадлежащая секущей плоскости и грани АВСD куба пересекает грань куба DD1C1C в точке Q, а грань куба AA1B1B в точке R.
Проведя прямую QG до пересечения с ребром D1C1, получим точку сечения Н.
Теперь можно провести НI параллельно EF и IK параллельно GF => получим все точки сечения.
Но можно построить недостающие точки P и S (построение понятно из рисунка) и провести прямые SI (через Н) и РК (через Е). Получим то же самое сечение, которое в силу симметричности точек является правильным шестиугольником.
1) угол на А/2 равен с углом при пересечении биссектрисы стороны ВС как накрест лежащие..отсюда получается равнобедренный треугольника..значит боковая сторона тоже равна 4..= ВК
ВС = 4+3 = 7, Р = 2(7+4) = 22
2)отметим 1-ю высоту как 4х , а вторую как 3х. из периметра найдем а+b = 42
а - меньшая сторона, b - большая.
найдем площадь S = 4x*a
еще одну площадь S = 3x*b
приравняем: 3хb = 4xa, b = 4a/3
подставим в а+b = 42, а+4а/3 = 42, 7а/3 = 42, а = 18
значит 18+b = 42, b = 42-18 = 24
меньшая сторона равна = 18
большая = 24
У квадрата диагонали перпендикулярны.
Центр окружности - это пересечение диагоналей в одной точке.
Например, обозначим квадрат АВСD и центр О(пересеч. диагоналей)
ВОС- прямоугольный треугольник
ВО=ВС
Найдем ВО и ОС по теореме Пифагора:
x^2+x^2=(6√2)^2
2x^2=36*2
2x^2=72
x^2=36
x=6
ВО=ОС=6
Радиус=ВО=ОС=6
ответ:6