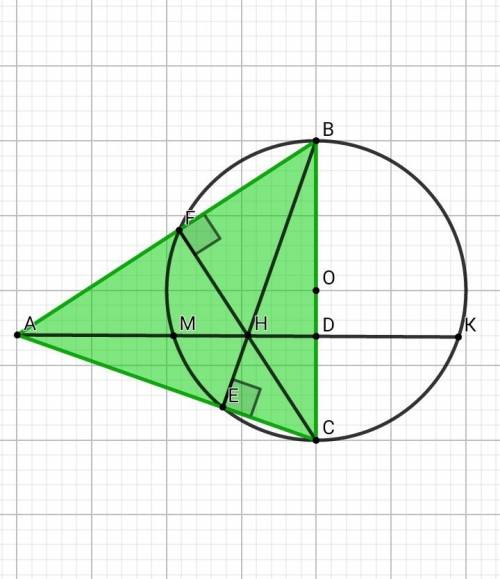
На стороне BC остроугольного треугольника ABC (AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 32, MD = 8, H — точка пересечения высот треугольника ABC. Найдите AH.
Решение.
Проведём построения и введём обозначения как указано на рисунке. Угол — вписанный, опирающийся на диаметр, поэтому он равен 90°. Значит, точка пересечения прямых и — точка пересечения высот Продолжим высоту до пересечения с окружностью в точке Получаем, что По теореме о секущих получаем, что Треугольники и — прямоугольные, угол — общий, следовательно, эти треугольники подобны, откуда:
ответ: 30.
Рассмотрим тр. AMD и BMCA1D1 - сред. линия тр. AMD, не принадлежит ABCD, A1D1 || ADB1C1 - сред. линия тр. BMC, не принадлежит ABCD, B1C1 || BC по условию BC||AD ⇒ A1D1 || B1C1ч.т.д.
AD:BC=5:3KL - ср. линия трап. = 16 смA1D1 - ?B1C1 - ?
Введем переменную x ⇒ AD=5x, BC=3x
Тогда по формуле средней линии трапеции:
16=(5x+3x)/232=8x
x=4
AD=5*4=20 см
BC=3*4=12 см
Тогда:A1D1=1/2*AD=1/2*20=10 смB1C1=1/2*BC=1/2*12=6 см