32 см³
Объяснение:
Чтобы найти объем пирамиды, надо знать площадь основания и высоту пирамиды.
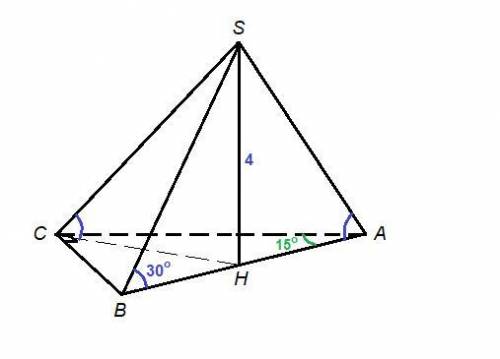
Проведем SH - высоту пирамиды. SH = 4 см.
Тогда АН, ВН и СН - проекции наклонных SA, SB и SC на плоскость основания соответственно.
∠SAH = ∠SBH = ∠SCH = 30°, значит прямоугольные треугольники равны ΔSAH = ΔSBH = ΔSCH по катету (SH - общий катет) и противолежащему острому углу. Следовательно
НА = НВ = НС, т.е. Н - это центр окружности, описанной около основания.
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.Итак, Н - середина гипотенузы АВ.
ΔSBH: ∠SHB = 90°,
ВН = SH · ctg 30° = 4√3 см
АВ = 2ВН = 2 · 4√3 = 8√3 см
ΔАВС: ΔАСВ = 90°, ∠ВАС = 15°
АС = АВ · cos 15° = 8√3 · cos 15°
BC = AB · sin 15° = 8√3 · sin15°
Площадь основания:
S = 0,5 · AC · BC
S = 0,5 · 8√3 · cos 15° · 8√3 · sin15°
Применим формулу синуса двойного угла:
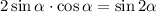
S = 4 · 3 · 4 · sin 30° = 48 · 0,5 = 24 см²
Объем пирамиды:
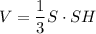
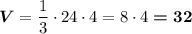 см³
см³
При симметрии относительно плоскости ОХУ координаты х и у точки не изменятся, а координата z поменяет знак на противоположный, так как симметричная точка будет находиться на таком же расстоянии от плоскости ОХУ, но с другой стороны.
Тогда центр сферы, точка с координатами (4; –2; 1) перейдёт в точку с координатами (4; –2; –1).
Уравнение сферы: (х – а)² + (у – b)² + (z – c)² = R²
(a; b; c) – координаты центра сферы, R – радиус сферы.
Тогда уравнение сферы с центром в точке с координатами (4; –2; –1) и радиусом 3 см примет вид:
(х – 4)² + (у + 2)² + (z + 1)² = 3²
(х – 4)² + (у + 2)² + (z + 1)² = 9
Найдём объём шара:
V = 4/3∙πR³
V = 4/3∙π·3³ = 4∙π·9 = 36π
В равнобедренном треугольнике биссектриса проведенная к основанию является высотой и медианой. Найдем длину основания треугольника:
√10²-8²=√100-64=√36=6 см, длина основания треугольника а= 2 *6 = 12 см.
радиус вписанной окружности: r=S/p
радиус описанной окружности: R = abc/4S
S= 12* 8 /2 = 48 cм²
p=(12 + 10 + 10)/2 = 16
r = 48/16 = 3 cм
R = 12 * 10 * 10 / (4*48) =25/4 = 6,25 cм