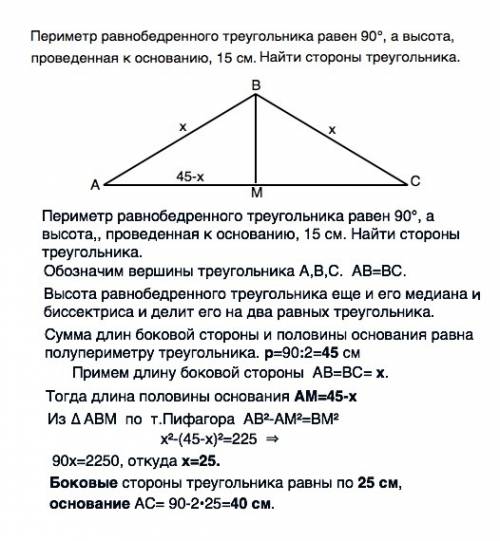
Периметр равнобедренного треугольника равен 90°, а высота,, проведенная к основанию, 15 см. Найти стороны треугольника.
Обозначим вершины треугольника А,В,С. АВ=ВС.
Высота равнобедренного треугольника еще и его медиана и биссектриса и делит его на два равных треугольника.
Сумма длин боковой стороны и половины основания равна полупериметру треугольника. р=90:2=45 см
Примем длину боковой стороны АВ=ВС= х.
Тогда длина половины основания АМ=45-х
Из ∆ АВМ по т.Пифагора АВ²-АМ²=ВМ²
х²-(45-х)²=225
90х=2250, откуда х=25.
Боковые стороны треугольника равны по 25 см,
основание АС= 90-2•25=40 см.
Пусть ABC - треугольник
AB = BC = 15см - боковые стороны
AC = 18см - основание
P = 24 см
Проведем высоту,медиану,биссектрису BH
Рассмотрим треугольник ABH - прямоугольный
BH = 12 ( по теореме пифогора )
Sabc = 1\2 BH AC = 108 см
r = S\p = 4.5см
R = abc\4S = 4050\432=9.375 см