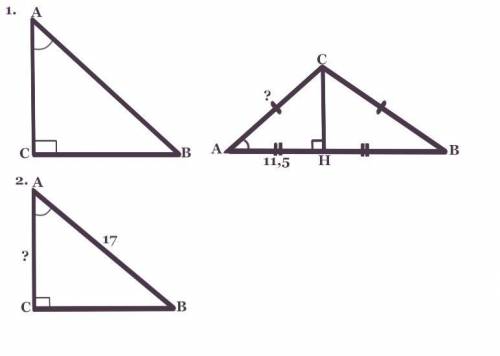
Дано :
ΔАВС - прямоугольный (∠С = 90°).
Найти :
Tg(∠A) = ?
Тангенс острого угла прямоугольного треугольника - это отношение противолежащего катета к прилежащему катету.Для ∠А :
Катет СВ - противолежащий
Катет АС - прилежащий.
Тогда по выше сказанному -
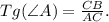
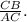
- - -
2)Дано :
ΔАВС - прямоугольный (∠С = 90°).
АВ = 17.
Найти :
АС = ?
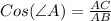 (по определению косинуса острого угла прямоугольного треугольника).
(по определению косинуса острого угла прямоугольного треугольника).
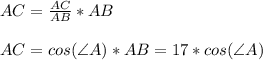
ИЛИ :

(Так как sin(∠B) = cos(∠A), то есть это одни и те же функции).
17*cos(∠A) или 17*sin(∠B).
- - -3)Дано :
ΔАВС.
АС = ВС.
АВ= 23.
Найти :
АС = ?
Так как АС = ВС (по условию), то ΔАВС - равнобедренный (по определению).
Проведём из вершины С на основание АВ высоту СН, которая по свойству высоты в равнобедренном треугольнике, проведённой к основанию, является медианой.
Тогда по определению медианы -
АН = НВ = 0,5*АВ = 0,5*23 = 11,5.
Рассмотрим ΔАНС - прямоугольный.
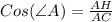 (по определению косинуса острого угла прямоугольного треугольника).
(по определению косинуса острого угла прямоугольного треугольника).
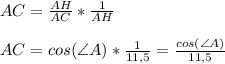
ИЛИ :
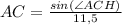
(так как sin(∠АСН) и cos(∠A) - одни и те же функции).
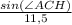 или
или 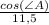 .
.
1) Количество граней = n + 2.
n - боковые грани, 2 - основания призмы.
2) Количество ребер = 3n.
Если посмотреть на любую призму, то сразу видно, что из любой вершины выходит по 3 ребра - 1 боковое и 2 в основании.
3) Количество вершин = 2n.
У каждого основания будет n вершин (например, у шестиугольника их 6), а всего оснований у нас 2.
Треугольная призма имеет 3 + 2 = 5 граней, 3 * 3 = 9 ребер и 2 * 3 = 6 вершин.
Четырехугольная призма имеет 4 + 2 = 6 граней, 3 * 4 = 12 ребер и 2 * 4 = 8 вершин.
Шестиугольная призма имеет 6 + 2 = 8 граней, 3 * 6 = 18 ребер и 2 * 6 = 12 вершин.
в восьмом классе доказательство могло бы выглядеть так:
если получившийся треугольник DВС -- прямоугольный, то
должна выполняться т.Пифагора:
DC² = 5² - 3² = 25-9 = 4² ((египетский треугольник со сторонами 3-4-5)))
и с другой стороны
DC² = (√17)² - 1² = 17-1 = 4² -- противоречия не возникает ⇒
DC _|_ AB
в 9 классе можно использовать т.косинусов...
из треугольника ADC можно записать:
(√17)² = 1² + DC² - 2*DC*cos(ADC)
DC² = 16 + 2*DC*cos(ADC)
из треугольника BDC можно записать:
5² = 3² + DC² - 6*DC*cos(BDC)
DC² = 16 + 6*DC*cos(BDC) = 16 + 6*DC*cos(180 - АDC) =
= 16 - 6*DC*cos(АDC)
и очевидно получается:
16 + 2*DC*cos(ADC) = 16 - 6*DC*cos(АDC)
2*DC*cos(ADC) = -6*DC*cos(АDC)
cos(ADC) = -3*cos(АDC) или cos(ADC) + 3*cos(АDC) = 0
4*cos(АDC) = 0 ⇒ cos(АDC) = 0
т.е. угол АDC = 90 градусов)))