Трапеция АВСД является равнобедренной, т.к. окружность описать можно только вокруг равнобедренной трапеции. Значит, АВ=СД=13 см.
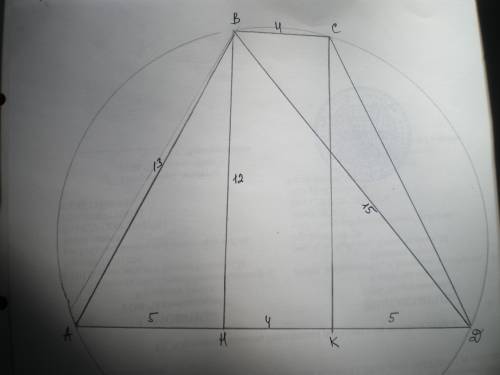
Проведем высоты ВН и СК. Тогда НК=ВС=4 см, АН=КД=(14-4):2=5 см.
Рассмотрим ΔАВН - прямоугольный. ВН=√(АВ²-АН²)=√(169-25)=√144=12 см.
Рассмотрим ΔАВД и найдем его площадь:
S=1\2 * АД * ВН= 1\2 * 14 * 12=84 см².
Из ΔВДН найдем ВД по теореме Пифагора ВД=√(ВН²+ДН²)=√(144+81)=√225=15 см
Найдем радиус окружности, описанной вокруг ΔАВД (этим же радиусом описана окружность вокруг трапеции АВСД)
R =(АВ*ВД*АД)/(4*S)=13*15*14\4*84=8,125 см
Найдем длину окружности по формуле С=2πR=2π*8,125=16,25π см
ответ: 16,25π см.
второе- нет (средняя линия трапеции равна полу сумме ее оснований)
третье-нет(во, первых такого признакам подобия не существует(есть по 2-М углам, по трем пропорциональным сторонам, по углу и двум пропорциональным сторонам, во-вторых можно нарисовать два треугольника, у которых будут равны по 2 стороны, но угол между ними будет разным. Поэтому треугольники не являются подобными или равными)
в итоге, к сожаленью, ты неверно ответил на это задание.