Question

Решить . боковые ребра правильной треугольной пирамиды sabc наклонены к плоскости основания под углом 45 градусов. шар касается плоскости основания abc в точке a и, кроме того касается вписанного в пирамиду шара. через центр первого шара и высоту bd основания проведена плоскость. найти угол наклона этой плоскости к плоскости основания.

Answer 1

(Нудная задача. Здесь и далее курсив можно не читать.)
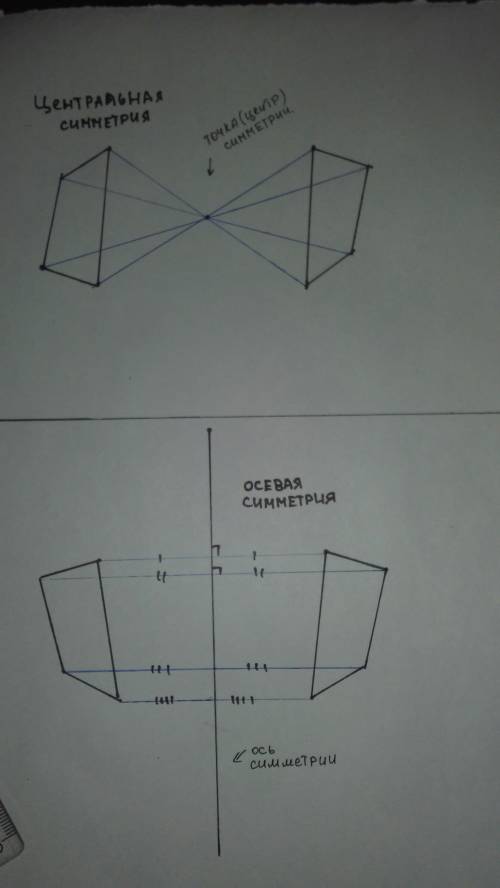
Центр вписанного шара O1 проектируется на основание ABC в центр правильного треугольника ABC (пусть это O2) - это следует из того, что пирамида "переходит в себя" при повороте вокруг SO2 на 120°; Далее, линия соединяющая центры шаров OO1 проектируется на основание на отрезок AO2. Этот отрезок - радиус описанной вокруг ABC окружности, он равен удвоенному радиусу вписанной в ABC окружности и равен высоте пирамиды, поскольку ребро наклонено к основанию под углом в 45°. Далее, прямая BD - это то же самое, что и прямая O2D, где D - середина AC. Ясно, что O2D перпендикулярно плоскости AOD, так как перпендикулярно двум прямым в этой плоскости - AC и OA (OA перпендикулярно всей плоскости ABC).
Поэтому нужный угол - это угол ADO, и для его вычисления надо найти радиус шара с центром в O.
Я обозначу этот радиус R, а радиус вписанного в пирамиду шара r.
1) Пусть радиус ВПИСАННОЙ в ABC окружности равен 1.
То есть O2D = 1; (Это не ограничивает общность.)
Тогда AO2 = 2 = SO2;
сторона основания равна 2√3;
площадь правильного тр-ка в основании Sabc = (2√3)^2*√3/4 = 3√3;
апофема равна SD = √(2^2 + 1^2) = √5;
площадь боковой грани равна 2√3*√5/2 = √15;
площадь полной поверхности пирамиды равна Spol = 3√3(√5 + 1);
объем пирамиды равен V = Sabc*SO2/3 = (3√3)*2/3 = 2√3;
отсюда радиус вписанного в пирамиду шара равен r = 3V/Spol = 2/(√5 + 1);
(Это соотношение совершенно аналогично известному S = pr для треугольника. И получается оно точно так же - надо соединить центр вписанного шара с вершинами и рассматривать пирамиду как сумму - в данном случае - четырех пирамид с высотами, равными радиусу вписанного шара. Отсюда V = Spol*r/3;)
2) Фигура AOO1O2 - прямоугольная трапеция. Её основания равны R и r, а боковые стороны R + r и 2 (вот здесь учитывается касание шаров, ясно, что точка касания лежит на линии центров). Поскольку r уже вычислено, найти R нетрудно. 
(R + r)^2 = (R - r)^2 + 2^2; или 4Rr = 4; R = 1/r; (занятное соотношение);
R = (√5 + 1)/2;
поскольку AD = √3; то искомый угол ADO = Ф имеет тангенс
tg(Ф) = (√5 + 1)/2√3;