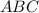
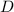 ∈
∈ 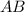
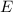 ∈
∈ 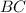
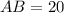 см
см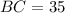 см
см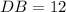 см
см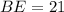 см
см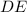 ║
║ 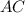
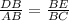
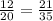
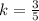
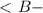 общий
общий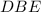 подобен Δ
подобен Δ 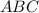
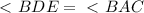
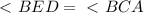
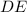 ║
║ 

Відповідь:
Пояснення:
Діагоналі куба в точці перетину діляться навпіл і ця точка рівновіддалена від усіх вершин, від усіх ребер, від усіх граней куба. Тобто, ця точка - центр симетрії куба. Тому фігура утворена в результаті перетину площиною альфа куба буде КК1N1N -квадрат, де О є центром квадрату, перетину діагоналей КN1 та К1N.
- в квадраті діагоналі перетинаються під прямим кутом, тому КОN=90
Або
- |КО|=|ОN| і діагоналі в квадраті є бісектрисами. Тоді трикутник КОN є рівнобедренним при основі кути рівні і =45 тому КОN=90
ΔА₁В₁С₁, ∠А₁С₁В₁ = 90°
АВ = А₁В₁, ВС = В₁С₁
Доказать: ΔАВС = ΔА₁В₁С₁
Доказательство:
Приложим треугольники равными катетами (см. на рис.)
Получим равнобедренный треугольник АВА₁, в котором ВС является высотой, а, следовательно, и медианой.
Значит, АС = А₁С₁. Тогда ΔАВС = ΔА₁В₁С₁ по трем сторонам.
Что и требовалось доказать.