Четырёхугольник ABCD - равнобедренная трапеция (ВС║AD, AD > ВС, АВ = CD).
Отрезок ВН - высота, опущенная на основание AD (ВН⊥AD, ВН⊥ВС).
Отрезок МК - средняя линия.
AH : HD = 1 : 5.
HD = 35 см.
Найти :МК = ?
Решение :На основание AD из вершины тупого ∠С опустим высоту СН₁ (СН₁⊥AD, СН₁⊥ВС).
По свойству отрезков в равнобедренной трапеции, образованных основанием высоты на большем основании :
АН = DH₁.
Пусть АН = х, тогда, по условию задачи, HD = 5х.
HD = 5х
35 см = 5х
х = 35 см/5
х = 7 см.
АН = DH₁ = х = 7 см
AD = AH + HD = 7 см + 35 см = 42 см.
Рассмотрим четырёхугольник BHH₁C.
Все его углы прямые, значит, этот четырёхугольник - прямоугольник (признак прямоугольника).
AD = AH + HH₁ + DH₁
HH₁ = AD - AH - DH₁ = 42 см - 7 см - 7 см = 28 см.
Тогда ВС = НН₁ = 28 см (так как противоположные стороны прямоугольника равны).
Средняя линия трапеции равна полусумме её оснований.Следовательно :
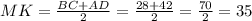 cм.
cм.
35 см.
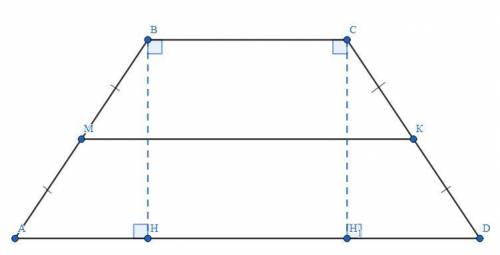
r = (a+b-c) / 2
т.к. катеты равны ⇒ a=b
r = a - c/2
по т.Пифагора
с² = a² + b² = 2a²
c = a√2
r = a - a√2 / 2 = a*(2 - √2) / 2
r = (54 + 27√2) * (2 - √2) / 2 = 27 * (2 + √2) * (2 - √2) / 2 = 27 * (4 - 2) / 2 = 27