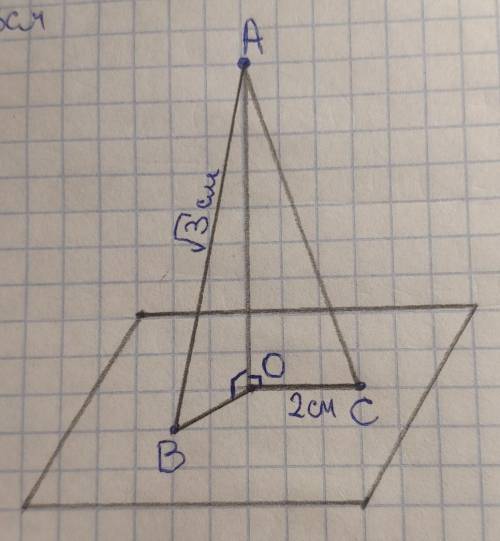
Прямая, перпендикулярная плоскости, перпендикулярна всем прямым, лежащим на этой плоскости.
Следовательно угол АОВ=угол АОС=90°, значит ∆АОВ и ∆АОС – прямоугольные.
ВО+АС=3 см по условию. Пусть ВО=х, тогда АС=3–х.
В прямоугольном ∆АОВ по теореме Пифагора:
АВ²=АО²+ВО²
(√3)²=АО²+х²
АО²=3–х² (Ур 1)
По теореме Пифагора в прямоугольном ∆АОС:
АС²=ОС²+АО²
(3–х)²=2²+АО²
АО²=9–6х+х²–4
АО²=х²–6х+5 (Ур 2)
Подставим значение АО² из уравнения 1 в уравнение 2, получим:
3–х²=х²–6х+5
2х²–6х+2=0
х²–3х+1=0
Д=(–3)²–4*1*1=9–4=5
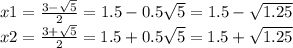
Тогда ВО=1,5+√1,25 или ВО=1,5–√1,25
Катет прямоугольного треугольника всегда меньше гипотенузы, то есть ВО<АВ
1,5+√1,25<√3
1,5+1,118<1,732
2,618<1,732
Неверно
1,5–√1,25<√3
1,5–1,118<1,732
0,382<1,732
Верно, следовательно ВО=1,5–√1,25 см.
Тогда АС=3–(1,5–√1,25)=3–1,5+√1,25=1,5+√1,25
ответ: ВО=1,5–√1,25 см, АС=1,5+√1,25 см.
1) Диагонали параллелограмма равны. НЕВЕРНО
Диагонали равны только у разновидностей параллелограмма : у прямоугольника и квадрата.
2) Катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы. ВЕРНО
3) В прямоугольной трапеции ровно один прямой угол. НЕВЕРНО
Боковая сторона, которая образует прямой угол с одним основанием трапеции, является перпендикуляром к двум параллельным основаниям, значит, она образует прямой угол со вторым основанием тоже. Всего в прямоугольной трапеции 2 прямых угла. Если в трапеции будет 4 прямых угла, то это будет прямоугольник.
4) Сумма углов четырёхугольника равна 360°. ВЕРНО
Треугольник ВЕД - равнобедренный (ВЕ=ВД - отрезки касательных к окружности, проведённых из одной точки) =>
угол ВЕД = углу ВДЕ = (180-120):2=30 град.
ВО - биссектриса угла ЕВД. => угол ЕВО = 120:2=60 град
Треугольник ЕВО - прямоугольный (ЕО - радиус, проведённый в точку касания), sinЕВО=ЕО/ВО=sin60=√3/2,
ЕО/ВО=√3/2
ВО=ЕО/(√3/2)=2√3/(√3/2)=4 см