Модели смежных углов известны людям давно. Первое сведение об этих углах складывалось во время рассмотрения дорог или каналов, которые пересекаются, при возведении внутренних стен домов так же. Зато долгое время основное свойство смежных углов практически не использовали. Вертикальные углы рассматривал в своём учебнике Фалес. Очевидно, он открыл и доказал теорему о равенстве вертикальных углов. Смежные углы связаны ещё с одним определением прямого угла. (Первое представлялось в том, что этот угол, градусная мера которого 90о)
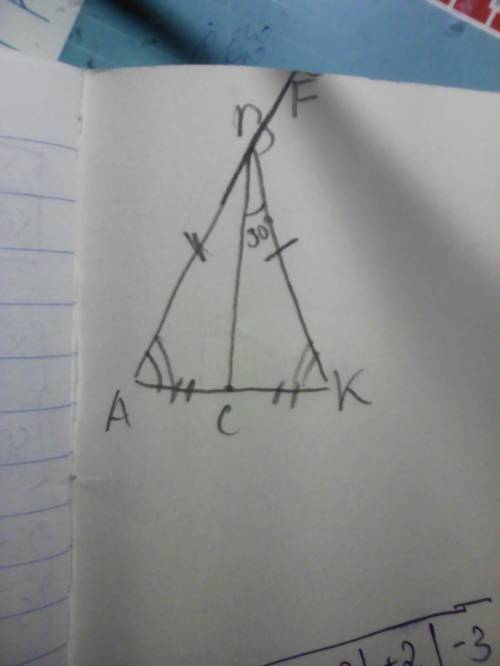
Рассм. ΔАВК
АВ = ВК по условию ⇒ ΔАВК - равнобедренный по определению
∠ А = ∠С по св-ву равнобедренного треугольника
Рассм. ΔАВС и ΔКВС
∠ А = ∠С по св-ву равнобедренного треугольника
АВ = ВК по условию
АС = СК по условию ⇒ ΔАВС = ΔКВС по двум сторонам и углу между ними, значит все их соответственные элементы равны, а в частности:
∠АВС = ∠СВК
∠СВК = 30° по условию ⇒ ∠АВС = 30°
Рассм. ΔАВК
∠АВС = ∠СВК = 30°
∠АВК = ∠АВС + ∠СВК = 30° + 30° = 60°
Сделаем дополнительное построение, продлим отрезок АВ дальше и назовём луч, который выходит из точки В, лучом ВF
∠ FBK и ∠ABK - смежные, по св-ву смежных углов ∠ FBK + ∠ABK = 180°, а ∠ABK = 60° ⇒ ∠ FBK = 180° - 60° = 120°
ответ: ∠ FBK = 120°
Площадь трапеции равна 8*6 = 48.
Высота призмы равна двум радиусам 3*2 = 6.
Тогда объём призмы равен 48*6 = 288.