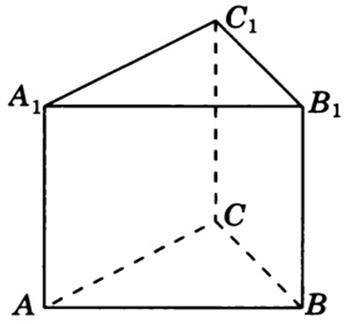
Нехай задана правильна трикутна призма, бічні грані якої є квадратами, а 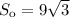 см² — площа основи цієї призми.
см² — площа основи цієї призми.
Основа призми є правильним (рівностороннім) трикутником зі строною  см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника:
см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника: 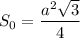
Отже, 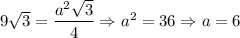 см.
см.
Через те що бічні грані є квадратами, тоді ребра призми дорівнюють 6 см (за властивістю квадрата) — ребра правильної призми є висотою призми.
Об'єм правильної трикутної призми можна розрахувати за формулою
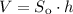 , де
, де 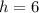 см — висота призми.
см — висота призми.
Знайдено значення шуканої величини:
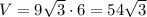 см³
см³
Відповідь: А) 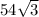 см³
см³
V=Sh:3
Площадь основания - площадь ромба и равна половине произведения диагоналей.
S=d*D:2=3*4:2=6 см²
Большее ребро -гипотенуза, половина диагонали и высота - катеты - это стороны прямоугольного треугольника.
h=(D/2):ctg(60°)=2:(1/√3)=2√3 см
V=(6*2√3):3=4√3 cм³